Forces acting on a mass sliding down an inclined plane – using vector resolution

Last updated on April 15th, 2021 at 03:10 pm

In this post, we will discuss the forces acting on a mass sliding down an inclined plane. To do this we will take the help of the concepts of Vector Resolution. Here we are not considering the presence of friction.

Forces acting on a mass sliding down an inclined plane

The first step when setting up the problem is to break down the force of weight into components.

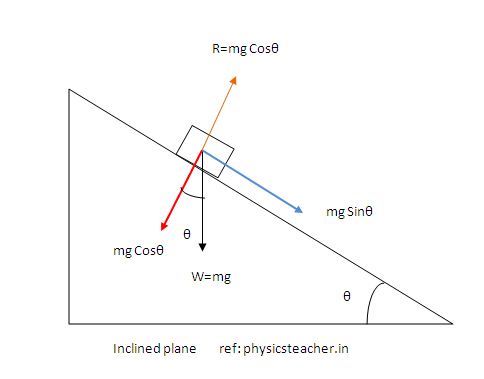
When an object rests on an incline that makes an angle θ with the horizontal, the force of gravity acting on the object is divided into two components:

1) A force (perpendicular weight component) acting perpendicular to the plane, mg Cosθ
2) And a second force (parallel weight component) acting parallel to the plane, mg Sinθ

Notice that the angle formed between W and the perpendicular weight component mg Cosθ is the same as the angle of the incline θ. [ can be proved easily using geometry concept as you consider the object as a point mass]

The perpendicular force of weight, mg Cosθ, is typically equal in magnitude and opposite in direction to the normal force (R in the diagram)

The force acting parallel to the plane, mg Sinθ, causes the object to accelerate down the incline.