Equipotentials between two oppositely charged parallel plates – explanation

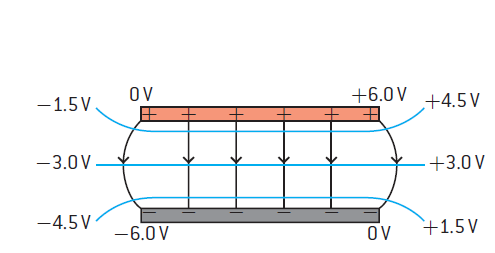
The lines of equal potential difference between two parallel plates resemble those shown in figure 1. These lines are called equipotentials because they represent points on two-dimensional paper where the voltage is always the same. When a charge moves from one point to another along an equipotential line, no work is done.

Figure 1 also shows the electric field lines between the plates.

There is a simple relationship between the field lines and the equipotentials. The angle between them is always 90°. If either the shape of the equipotential lines or the shape of the field lines is known then the shape of the other can be deduced.

Why is the angle between the electric field lines and the equipotentials is always 90°?

A Field line in an electric field represents the path followed by a unit positive charge under the influence of the net electric force in the electric field. Hence the direction of the field line is the same as the direction of the net force.

By definition, equipotentials are points in the electric field where the electric potential (voltage) is the same.

And hence, when a charge moves from one equipotential point to another along an equipotential line, no work is done.

By definition, of work when the direction of force and the direction of displacement are perpendicular to each other, then the work done equals zero. (W = Fs cos θ. And, when θ=90°, then W = 0)

This makes it clear that the angle between the electric field lines and the equipotentials is always 90°.