Instantaneous Velocity – definition & equation with solved problem

Last updated on May 8th, 2021 at 09:48 am

The quantity that tells us how fast an object is moving at a specific instant in time anywhere along its path is the instantaneous velocity, usually called velocity as well.

That means when we say ‘velocity’ of a body we actually mean instantaneous velocity.

Another related term is the average velocity that is basically for a duration of time and we have discussed it in another post.

What do we mean by Instantaneous Velocity?

The quantity that tells us how fast an object is moving at a specific instant in time anywhere along its path is the instantaneous velocity, usually called velocity as well.

Definition

The instantaneous velocity of an object is the limit of the average velocity as the elapsed time approaches zero, or the derivative of x with respect to t:
v(t) = dx(t)/dt.

Getting the Equation or Formula (step by step)

Instantaneous velocity is the average velocity between two points on the path in the limit that the time (and therefore the displacement) between the two points approaches zero. We will use the general formula of average velocity to find out the formula of Instantaneous velocity with the tweak of making the time elapsed nearly zero.

To illustrate this idea mathematically, we need to express position x as a continuous function of t denoted by x(t).

The expression for the average velocity between two points using this notation is
v = [x(t2) − x(t1)] / (t2 − t1)

To find the instantaneous velocity at any position, we let t1 = t and t2 = t + Δt.
As said earlier above, this Δt has to be near zero if we want to calculate instantaneous velocity.

After inserting these expressions into the equation for the average velocity and taking the limit as Δt → 0, we find the expression for the instantaneous velocity:

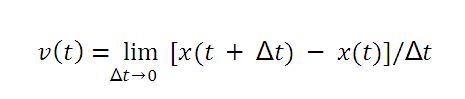
v(t) = dx(t)/dt.

Formula or equation of instantaneous velocity

v(t) = dx(t)/dt

So How to find velocity? | How to get instantaneous velocity?

By the term Velocity actually we mean Instantaneous Velocity. So by using the equation v(t) = dx(t)/dt, we can easily find the value of velocity or instantaneous velocity.

Sample numerical problems on instantaneous velocity physics – with solution

Q1.) The position of a particle is given by x(t) = 3.0t + 0.5t³ m .
a. find the instantaneous velocity at t = 2.0 s.

Solution:

a.
Here, x(t) = 3.0t + 0.5t³ m
So, v(t) = dx(t)/dt = 3.0 + 1.5t² m/s .

Substituting t = 2.0 s into this equation gives
v(2.0 s) = [3.0 + 1.5(2.0)2] m/s = 9.0 m/s .

Q2.) The altitude of a rocket in the first half-minute of its ascent is given by x = bt² where the constant b is 2.9 m/s^2. Find a general expression for the rocket’s velocity as a function of time and from it the instantaneous velocity at t = 20 seconds.

Solution: To find a general expression for the rocket’s velocity as a function of time, we have to use the equation of Instantaneous velocity.
so, Expression of Velocity = V = dx/dt.
Here, x = bt²

Hence, V = dx/dt = d(bt² )/dt = 2bt
V=2bt ……………..(1) [ general expression for the rocket’s velocity]

Using equation (1) we find instantaneous velocity at t = 20 seconds = 2 b t = 2*2.9* 20 = 116 m/s ……(2)
[ used the value of b, as given in Q]

Take Away

These physical quantities of the motion chapter look simple, but a good understanding and concept on these basic pillars of motion chapter are important.

Also Read: (suggested reading)

Difference between Instantaneous Speed and Instantaneous Velocity

Difference between average speed and average velocity

Instantaneous Velocity – definition & equation with solved problem

Average velocity – definition, formula

Instantaneous Acceleration – definition & formula with solved problem

Average Acceleration and its formula & solved numerical problems