Torque Formula – What is Torque, Calculation, Derivation
Last updated on April 19th, 2021 at 05:32 pm
The torque formula expressing Torque can be written in the following 3 ways:
1) The first formula of torque describes torque as the moment of force and expresses it as the cross product of Force and Lever Arm Length (Torque T=r xF)
2) The second torque formula expresses torque as the time rate change of angular momentum. T = ΔL/ΔT
3) The third formula of torque shows it as the cross product of the moment of inertia (I) and angular acceleration (Alpha). (T= I X α)
Torque is the Moment of Force (Rotational domain equivalent of Force). It is the determining factor of how effectively a force can twist or turn something.
This post is all about the torque formula sets, their step by step derivation and calculation of torque using formula while solving a numerical problem.

What is Torque?
Torque is the Moment of Force (Rotational domain equivalent of Force) which is the determining factor of how effectively a force can twist or turn something.
In the next sections, we will write three equations or formulas of torque again with a short description for each. And then we will derive all three equations one by one. This post is apt for students of class 11 and 12 (CBSE, ICSE and other international boards as well).
3 different forms of Torque formula in physics
The torque formula is presented here in 3 different forms and those are (1) torque as the moment of force (2) Torque as the time rate change of angular momentum, and (3) Torque as the time rate change of angular momentum.
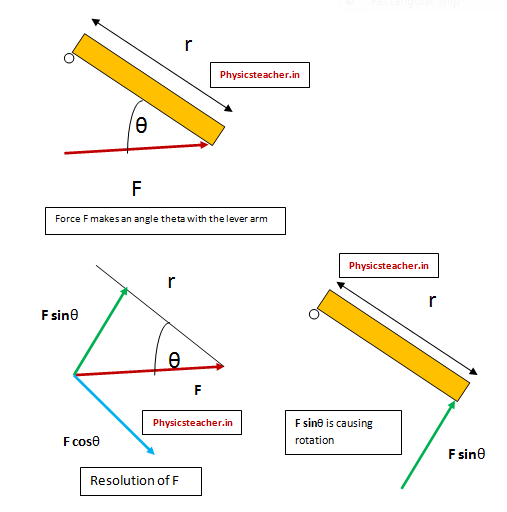
Formula of Torque in terms of Lever Arm Length (r) and the Force applied (F)
Torque formula can be framed considering Torque as the Moment of Force. It is the cross product of Lever Arm Length (r) and the Force applied (F).
T = r x F = r F Sin θ ………….(1)
Lever arm length r is the shortest distance between the rotation axis and the point of application of the force and θ = angle made between Lever arm and the line of action of the force being applied.
F Sin θ is the perpendicular component of the force which is the actual component of the applied force responsible for the rotation.
Formula of Torque in terms of rate of change of angular momentum
The second formula of Torque: Torque can also be defined as the time rate of change of angular momentum.
T = ΔL/ΔT …………(2)
Here ΔL is the change in angular momentum and ΔT is the time duration when this change happens.
Torque Formula in terms of Moment of Inertia(I) and Angular Acceleration(α)
The third Formula for torque: Torque is also expressed as the cross product of Moment of Inertia(I) and Angular Acceleration(α)
T= I X α ……………(3)
(Tao = I cross Alpha)
here, I stands for Moment of inertia and α is the angular acceleration
Derivation of Torque formula
Derivation of torque formula is done here in 3 different ways and shown in detail in the next 3 sections.
Derive formula of torque as the cross product of force and lever arm length.
This derivation of the T formula is based on our understanding of Torque as the Moment of force.
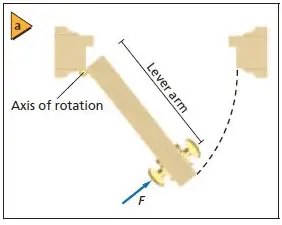
– When a Force is applied on a particle and that particle starts to rotate or tends to rotate about an axis then it is generally said that a Moment of force is generated.
– The lever arm is the perpendicular distance from the axis of rotation to the point where the force is exerted.
– If the force is applied perpendicular to the radius of rotation then the entire force F is responsible for the rotation
– But if the force is not perpendicular, the perpendicular component of the force must be found. Because this is the component that causes rotation in this case.
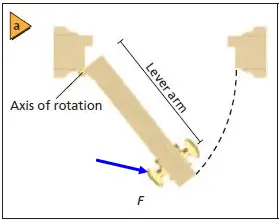

Thus we get Torque = r F sin(Theta) = r X F
From the above diagram, we can see that as the F (in red arrow) is applied at an angle theta with the lever arm(in yellow), the entire force F can’t act to create the rotation.
Rather, the effective force that generates torque = Vertically resolved component of F = F sinθ [The component in green in the above diagram].
Thus we get Torque = T = moment of force = product of lever arm length and the force component causing rotation = r F sinθ = r x F ………………(a)
Here, ‘X’ denotes Cross Product of vectors.
Therefore, we can write the expression of torque as the cross product of lever arm length r and the applied force F.
This is the formula we use to do Torque Calculation.
Note for quick revision:
Lever arm length r is the shortest distance between the rotation axis and the point of application of the force and θ = angle made between Lever arm and the line of action of the force being applied.
Derive the equation of Torque as the Rate of Change of Angular Momentum
We know that Rate of change of Angular Momentum with respect to time = ΔL/ΔT
Now, ΔL/ΔT = Δ(I ω)/ΔT = I. Δω/ΔT ……. (1)
[ Here “I” is constant when mass and shape of the object are unchanged]
Now Δω/ΔT is the rate of change of angular velocity with time i.e. angular acceleration (α).
So from the equation (1), we can write,
ΔL/ΔT = I α …………………(2)
Have you noticed this expression I α?
I (moment of inertia) is the rotational equivalent of mass(inertia) of linear motion.
Similarly, angular acceleration α (alpha) is the rotational motion equivalent of linear acceleration.
Product of mass m and linear acceleration a represents Force in linear motion.
Similarly, I and α in product form represent Torque (τ), which in turn is the rotational equivalent of Force.
So from equation (2), we get, ΔL/ΔT = τ ..…………..(b)
which states that the rate of change of angular momentum with time is called Torque. This is one τ equation.
This represents the relation between angular momentum and torque.
Derive formula of torque as the cross product of Moment of Inertia (I) and Angular Acceleration( α or Alpha)
In this post, we have seen that Torque (T) is the moment of force. Τ = r X F = r F sinθ …..(equation #a above)
Now expanding this by putting F = ma we get: (m = mass of the object, and a = linear acceleration)
Torque Τ = r F sin θ = r ma sinθ = r m αr sinθ = mr^2. α sinθ = I α sinθ
T= I X α ………………(c)
This is another τ equation.
[α (alpha) is angular acceleration, I is the moment of inertia and X denotes cross product.]
So τ is the cross product of I and α (alpha).
Solved Example on Torque Formula
Numerical Problem on Torque formula
Q1. A force of 800 N is applied to a heavy door to open it. The force is applied making an angle of 30 degree to the door. The lever arm length is 0.5 m. Find out the magnitude of the torque generated?
Solution:
T = F × r × sinθ
Here. force F = 800 N
r = lever arm length = 0.5 m
And the angle between the lever arm and the line of applied force is 30 degree => θ = 30
And sinθ = sin30 =1/2
Therefore, magnitude of the torque = F × r × sinθ =(800N) (0.5m) (1/2)= 200 N∙m
Hence, the magnitude of the torque generated is 200 N∙m.
The SI unit for torque is the newton meter (N⋅m).
Related Posts – must read
1> Definition and Practical Examples
