Torque Physics with definition and Examples

Last updated on February 12th, 2022 at 03:22 pm

Let’s start with Torque physics and the Definition of Torque is the first point of our discussion here. Torque is the Moment of Force (Rotational domain equivalent of Force). It is the determining factor of how effectively a force can twist or turn something. It is expressed as the cross product of force and the lever arm length.

In Physics, Torque is also defined as the rate of change of angular momentum. Torque can also be defined as the cross product of Moment of Inertia and Angular Acceleration.

Now if we have to understand the words in the first para above we need some examples from torque physics.

Table Of Contents

Torque physics and maximizing torque
In what direction to apply force to get max torque?
Where to apply the force for maximum torque as per Torque physics?
Torque is the moment of force
Conclusion
Related posts

Torque physics and maximizing torque

We will discuss this with some practical examples. Let’s first consider the Bank Vault door.

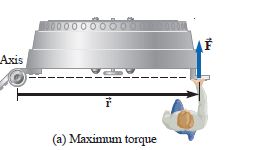
Now, What determines a torque produced by a particular force?

When we try to push open a massive bank vault door, certainly we would push as hard as we can. The torque certainly is proportional to the magnitude of the force.

But just by applying a huge force, we can’t expect to get a huge torque.

In torque physics, It also matters where and in what direction we are applying the force.

In what direction to apply force to get max torque?

Maximum torque when pushed perpendicularly [torque physics]

For maximum effectiveness, we have to push perpendicularly to the door ( Fig. a – above).

radial push generates zero torque [definition of torque]

If we push radially, i.e. straight in toward the axis of rotation that passes through the hinges, the door wouldn’t rotate, no matter how hard we push ( Fig. b ).

a force or push is resolved into horizontal and vertical components to find out the effective force causing the torque [definition of torque]

A force acting in any other direction can be decomposed into horizontal and perpendicular components, with the horizontal component contributing nothing to the torque ( Fig. c ). Only the perpendicular component of the force ( F ⊥ ) produces a torque.

Where to apply the force for maximum torque as per Torque physics?

Furthermore, where we apply the force is critical.

Instinctively, we would push at the outer edge, as far from the rotation axis as possible.
If we push close to the axis, it would be difficult to open the door.

Torque is proportional to the distance between the rotation axis and the point of application of the force (the point at which the force is applied). So to get more torque we have to push at the outer edge, as far from the rotation axis as possible.

We define the magnitude of the torque as the product of the distance between the rotation axis and the point of application of the force ( r ) with the perpendicular component of the force ( F ⊥ ):

Torque is the moment of force

So we can write, t = ±rF⊥
where r is the shortest distance between the rotation axis and the point of application of the force and F ⊥ is the perpendicular component of the force.

While opening a door that is free to rotate about its hinges, the greatest torque is produced when the force is applied farthest from the hinges and at an angle perpendicular to the door.

Conclusion

Here we have discussed torque physics with real-life examples and also discussed how a torque value can be maximized. We have published related tutorials and we are sure you will find those informative and useful as well. See the section below for their links.

Get more details about Torque physics.

formula and equations of torque with derivations