Relation between power and velocity | Force power velocity relationship
In mechanics, we can also express power in terms of force and velocity. In this post, we will derive the relation between power and velocity. First, we will follow a simpler method (for class 10). And then we will use the concept of Vector to find out the Force power velocity relationship.
Relation between power and velocity
Consider a vehicle traveling at constant velocity v along a straight, level road. The engine must continue to do work against friction as the vehicle is moving at a constant velocity.
If the frictional force is F, then the engine will supply an equal-sized force in the opposite direction.
The work done by the engine, W, in time t, is Fs, where s is the distance traveled in time t:
So, power = (Fs)/t ………………. (1)
but s/t= v,
therefore: power = Fv
Now, let’s find the above relationship involving vector concepts.
Force power velocity relationship [using vector concept]
Suppose that a force F acts on an object while it undergoes a vector displacement Δs. If F|| is the component of F tangent to the path (parallel to Δs), then the work done by the force is ΔW = F||Δs.
The average power is Pav =(F||Δs)/Δt = F|| (Δs/Δt) = F||vav ……………… (a)
Instantaneous power P is the limit of this expression as Δt ->0
P = F||v ………………(b)
where v is the magnitude of the instantaneous velocity.
We can also express Eq. (b) in terms of the scalar product: P = F.v
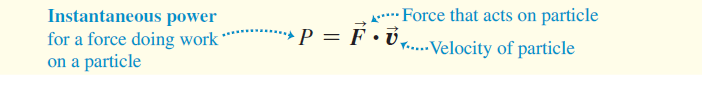
Numerical solved using P= Fv equation
A cyclist is travelling along a straight level road at a constant velocity of 27 km h−1 against total frictional forces of 50 N.
Calculate the power developed by the cyclist.
Solution:
First, let’s Convert the velocity from km h−1 into m s−1:
v= 27 km h−1 = 27 ×1000/3600 = 7.5 m s−1.
As the cyclist is moving with uniform velocity, hence Force applied by the cyclist = frictional force
So the power developed by the cyclist = force × velocity = 50 x 7.5 W = 375 W
