Conical Pendulum & Time period equation – derivation | Problem solved

Last updated on February 12th, 2022 at 10:06 am

We will discuss the following topics (1) What is a conical pendulum? (2) the time period of the conical pendulum – equation or formula of time period (3) Derivation of the time period equation of the conical pendulum (4) Diagram of a conical pendulum (5) find out the equation of tension in the string of a conical pendulum (6) find out the semi-vertical angle of a conical pendulum

---

What is a conical pendulum? | with diagram

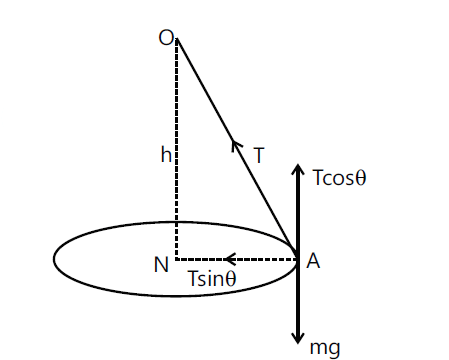
A conical pendulum consists of a string OA whose upper-end O is fixed and a bob is tied at the free end.

Say, a horizontal push is given to the pendulum bob by drawing it aside.

And, say it describes a horizontal circle with uniform angular velocity ω in such a way that the string makes an angle θ with the vertical.

Then the string traces the surface of a cone of semi-vertical angle θ.

It is called a conical pendulum. In diagram (1) below, the angle AOH equals θ.

Tension in the string & length of the string (conical pendulum)

Let us assume that T be the tension in the string, l be the length and r be the radius of the horizontal circle described.

Now, the vertical component of tension balances the weight, whereas the horizontal component supplies the centripetal force.

Derive the Time period equation for Conical Pendulum

The angle AOH equals θ.

From diagram 1 above, Tcosθ = mg ; [vertical component of tension balances the weight]

Tsinθ = mrω² [horizontal component of tension supplies the centripetal force]

∴ tanθ = (Tsinθ )/(Tcosθ) = rω² / g

ω = (gtanθ / r )^1/2 ………………… (1)

Again, r= lsinθ …………..(2)

Also, ω = 2π / t …………… (3) [t is the time period, i.e., time for one revolution.
We have used capital T as tension in the string, hence to avoid confusion we will use small t as the time period in the derivation part.]

from equation 1, 3 & 2 we get,
2π / t = (gtanθ / r )^1/2

=> 2π / t = (gtanθ / lsinθ )^1/2

t = 2π ( lcosθ/g ) ^½

t = 2π (h / g )^1/2 where h = l cosθ = height of the cone

Thus we have derived the equation of the Time Period of the conical pendulum as, Time Period = 2π (h / g )^1/2

Time period equation of conical pendulum

Time Period = T = 2π (h / g )^1/2

How to find out the Tension in the string of a conical pendulum

You can use either of the following equations to find out the value of tension T in the string. Pls, note that T denotes tension here.

– From diagram 1 above, T cosθ = mg ; [vertical component of tension balances the weight]
– And, T sinθ = mrω² [horizontal component of tension supplies the centripetal force]

How to find out the semi-vertical angle θ of a conical pendulum

Use any of the following equations according to the dependent data provided in the problem statement to find out the value of θ:

T cos θ = mg …… (a)
T sin θ = mrω² … (b)
tan θ = (T sin θ )/(T cos θ) = rω² / g

θ = tan^-1 (rω² / g)…………… (c)