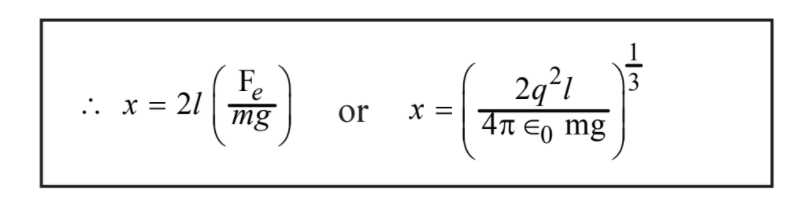Identically Charged spheres of the same mass vertically suspended are in equilibrium – derive formulas

Say, two Identically Charged spheres of the same mass are suspended vertically and they got to be in equilibrium. Now, here we will derive the formulas related to this equilibrium condition.

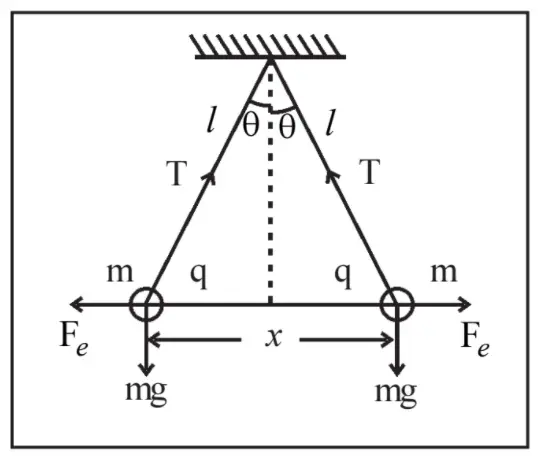
As shown in figure 1, let the spheres be of mass m and each of these is charged with charge q. These are suspended vertically from the same point with two separate strings. Being identically charged they will repel each other, and say at the time of equilibrium the distance between the spheres be x. And say, each of the strings makes an angle of θ with the vertical line.

tan θ = (x/2)/l = x/(2l) ……………. (1)

Again, using geometry, tan θ = F_e/(mg) ………..(2) [ refer to figure 1]

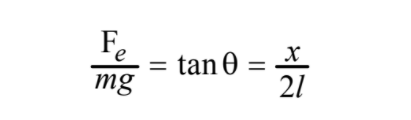
Merging equation (1) and (2) we get

x/(2l) = F_e/(mg)

x = (2l) F_e/(mg) ……………. (3)
[So this is the distance between the two masses when they are in equilibrium.]

Now, F_e = q²/(4πε₀)r²

Putting this expression for F_e in equation (3) we get a modified equation of x as

x = [ 2q² l / (4πε₀ mg)]^1/3 …………………. (4)