Electric Field due to a Uniformly Charged Spherical Shell & solid sphere

Last updated on November 21st, 2022 at 10:51 am

In this post, we will derive (1) the expression of the Electric Field due to a Uniformly Charged Spherical Shell, and (2) the expression of the Electric Field due to a Charged solid sphere.

A spherical shell, by definition, is a hollow sphere having an infinitesimal small thickness.

First, we will consider a spherical shell of radius R carrying a total charge Q which is uniformly distributed on its surface. We shall calculate the electric field due to the spherical charge distribution at points external as well as internal to the shell.

Later, we will also discuss whether this electrical field formula remains the same if we take a charged solid sphere instead of a hollow spherical shell.

---

(a) Electric Field due to a Uniformly Charged Spherical Shell at an external point

Let P be an external point at a distance r from the center O of the shell.

Let’s draw a spherical surface (called Gaussian surface) passing through P and concentric with the charge distribution. The radius of the spherical surface will obviously be r.

By symmetry, the electric field is radial, being directed outward as shown in Fig. 1.

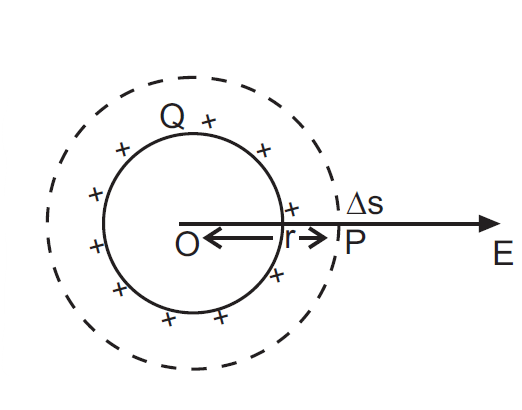
The electric field E is normal to the surface element Δs everywhere on the Gaussian surface passing through P.

Its magnitude at all points on the Gaussian surface has the same value E.

According to Gauss’ law,

ΣEΔs cos 0° = Q/ε₀

E A = Q/ε₀

E 4πr² = Q/ε₀

E = Q/(4πε₀r²)
( Electric Field due to a Uniformly Charged Spherical Shell at an external point )

From the result, we can conclude that for a point external to the spherical shell, the entire charge on the shell can be treated as though located at its center. The electric field decreases with distance.

(b) Electric Field due to a Uniformly Charged Spherical Shell at any point on its surface

Here, we will be able to use the formula for the Electric Field due to a Uniformly Charged Spherical Shell at an external point, with the value of r equal to R (radius of the spherical shell).

That means, Electric Field due to a Uniformly Charged Spherical Shell at any point on its surface E_surface= Q/(4πε₀R²)
where R = radius of the shell.

(c) Electric Field due to a Uniformly Charged Spherical Shell at an Internal Point

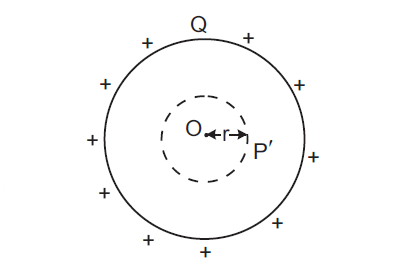
Let P′ be an internal point distant r from the center of the shell. (refer to figure 2) Draw a concentric sphere passing through the point P′.

The electric field E is normal to the surface element Δs everywhere on the Gaussian surface passing through P′.

Its magnitude at all points on this Gaussian surface has the same value E.

Applying Gauss’ Law,

ΣEΔs cos 0° = Q/ε₀

E A = Q/ε₀

E 4πr² = Q/ε₀ ……………. (i)

For a spherical shell, all charges reside only on the surface.

Hence, at an internal point of the spherical shell charge Q = 0.

As a result, we get from equation (i) above that the electric field E at an internal point of the shell is zero.

E = 0 ( Electric Field due to a Uniformly Charged Spherical Shell at an Internal Point )

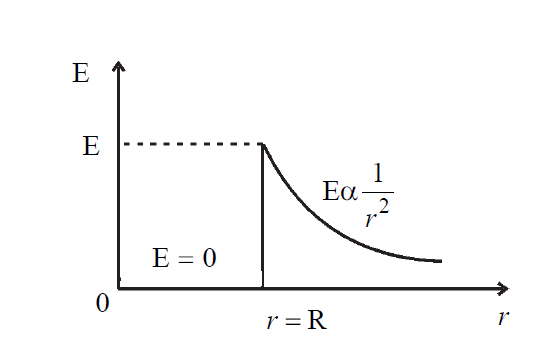
Uniformly Charged Spherical Shell – Graphical representation of the electric field with radial distance

Here is the Graphical representation of the electric field with radial distance for a Uniformly Charged Spherical Shell. R is the radius of the sphere. When r < R, the electric field E = 0.

(d) Electric Field due to a Uniformly Charged solid conducting sphere at an external point

Instead of a spherical shell, let’s take a Uniformly charged solid conducting sphere of radius R. For a conducting sphere entire charge will reside on the surface of the sphere only, being uniformly distributed.

Let’s try to find out the electric field at an external point (at a distance r from the center of the solid sphere, where r>Radius of the solid conducting sphere).

In this case, we would obtain the same result as we find for a Uniformly Charged Spherical Shell for an external point.

This is because the charge Q is enclosed fully by the imaginary spherical surface (called Gaussian surface) of radius r (where r>R).

Hence, Electric Field due to a Uniformly Charged solid conducting sphere at an external point is:
E = Q/(4πε₀r²)

(e) Electric Field due to a Uniformly Charged solid conducting sphere at any point on its surface

Here, we will be able to use the formula for the Electric Field due to a Uniformly Charged solid conducting sphere at an external point, with the value of r equal to R (radius of the spherical shell).

That means, Electric Field due to a Uniformly Charged solid conducting sphere at any point on its surface E_surface= Q/(4πε₀R²)
where R = radius of the shell.

(f) Electric Field due to a Uniformly Charged solid conducting sphere at an internal point

As said above, for a conducting sphere entire charge will reside on the surface of the conducting sphere only, being uniformly distributed. Hence, if we want to determine the electric field at any internal point of it and draw an imaginary Gaussian surface through that internal point, then we will find no charge enclosed by that surface.

Hence, if we apply the Gauss theorem, we will find the Electric Field due to a Uniformly Charged solid conducting sphere at an internal point = 0. (same as the spherical shell – see above)

Uniformly Charged solid conducting sphere – Graphical representation of the electric field with radial distance

Here is the Graphical representation of the electric field with radial distance for a Uniformly Charged solid conducting sphere. R is the radius of the sphere. When r < R, the electric field E = 0.

(g) Electric Field due to a Uniformly Charged nonconducting solid sphere at an external point

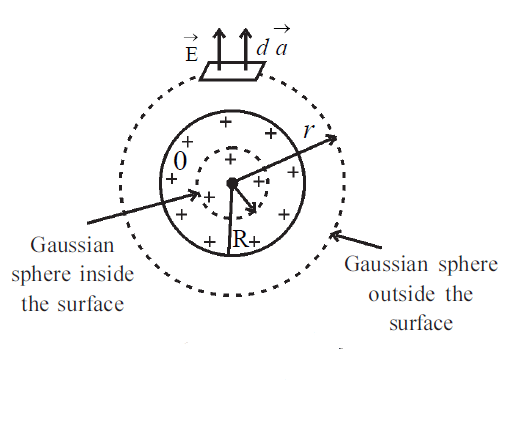
As in this case, the solid sphere is nonconducting, the charges will remain distributed within the sphere’s volume. (won’t come to the surface)

But for an external point at a distance r from the center when a Gaussian surface is drawn, the entire charge will be enclosed by that surface.

Hence, using the Gauss Theorem, we can find the Electric Field due to a Uniformly Charged nonconducting solid sphere at an external point as E = Q/(4πε₀r²)

(h) Electric Field due to a Uniformly Charged nonconducting solid sphere at an internal point

For point lying inside the sphere : (again refer to figure 5 above )

Imagine a spherical Gaussian surface of radius r where r<R.

The charge Q is uniformly distributed in the sphere of radius R. (volume distribution)

So the charge q contained by the internal sphere of radius r (where r<R) can be obtained as:

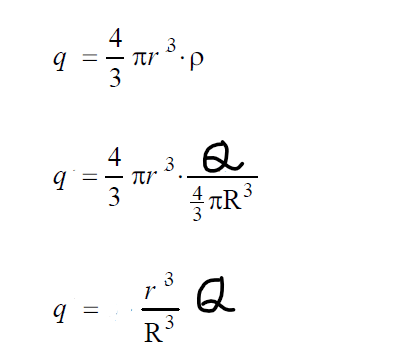
Applying Gauss’ Law,

ΣEΔs cos 0° = q/ε₀

E. 4πr² =[Q r³/R³ ]/ε₀

=> E = (1/4πε₀) [Q r/R³ ]

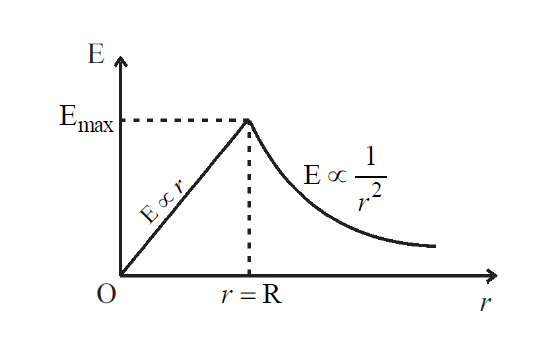
Uniformly Charged nonconducting Solid Sphere – Graphical representation of the electric field with radial distance

Here is the Graphical representation of the electric field with radial distance for a Uniformly Charged nonconducting Solid Sphere. R is the radius of the sphere.

Formulas of Electric Field due to a Uniformly Charged Spherical Shell

Electric Field due to a Uniformly Charged hollow Spherical Shell at an external point E = Q/(4πε₀r²)

Electric Field due to a Uniformly Charged hollow Spherical Shell at an Internal Point E = 0

Formulas of Electric Field due to a Uniformly Charged conducting solid sphere

Electric Field due to a Uniformly Charged solid conducting sphere at an external point E = Q/(4πε₀r²)

Electric Field due to a Uniformly Charged solid conducting sphere at an internal point E = 0

Formulas of Electric Field due to a Uniformly Charged nonconducting solid sphere

Electric Field due to a Uniformly Charged solid nonconducting sphere at an external point E = Q/(4πε₀r²)

Electric Field due to a Uniformly Charged solid nonconducting sphere at an internal point E = (1/4πε₀) [Q r/R³ ]