Series Combination of capacitors
Series Combination of capacitors
Two capacitors connected as shown in Figure 1a and the equivalent circuit diagram in Figure 1b are known as a series combination of capacitors. The left plate of capacitor 1 and the right plate of capacitor 2 are connected to the terminals of a battery. The other two plates are connected to each other and to nothing else; hence, they form an isolated conductor that is initially uncharged and must continue to have zero net charge.
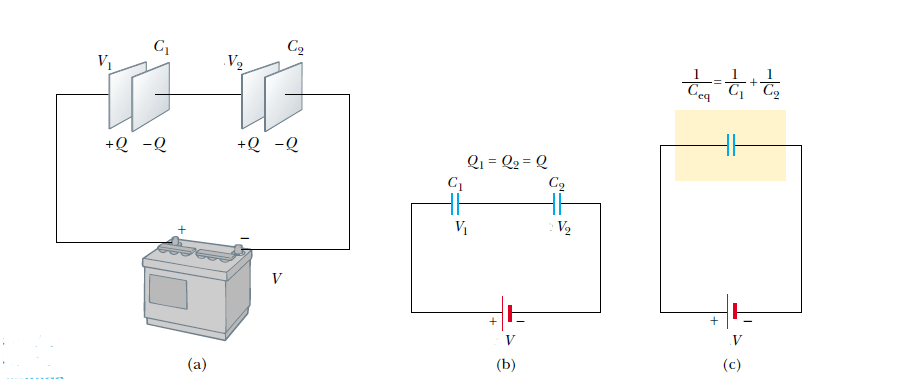
(c) The equivalent capacitance can be calculated from the relationship shown in figure 1c.
Let us consider the uncharged capacitors and discuss what happens just after a battery is connected to the circuit.
When the battery is connected, electrons are transferred out of the left plate of C1 and into the right plate of C2. As this negative charge accumulates on the right plate of C2, an equivalent amount of negative charge is forced off the left plate of C2, and this left plate therefore has an excess positive charge. The negative charge leaving the left plate of C2 causes negative charges to accumulate on the right plate of C1. As a result, all the right plates end up with a charge -Q , and all the left plates end up with a charge +Q . Thus, the charges on capacitors connected in series are the same.
Characteristics of Series Combination of capacitors
- The charges on capacitors connected in series are the same.
- The total potential difference across any number of capacitors connected in series is the sum of the potential differences across the individual capacitors.
- The inverse of the equivalent capacitance is the algebraic sum of the inverses of the individual capacitances and the equivalent capacitance of a series combination is always less than any individual capacitance in the combination. 1/Ceq=1/C1 + 1/C2 + 1/C3+…. ( see derivation of equivalent capacitance of a series combination of capacitors)
- When two or more capacitors are connected in series, they carry the same charge, and the sum of the potential differences equals the total potential difference applied to the combination. The sum of the reciprocals of the capacitances equals the reciprocal of the equivalent capacitance, which is always less than the capacitance of the smallest individual capacitor.

