Derive an expression for the potential energy of elastic stretched spring

Last updated on April 14th, 2021 at 04:56 pm

Here we will obtain or derive an expression for the potential energy of elastic stretched spring. This energy is also known as elastic potential energy. To get this equation, we’ll calculate the work done to stretch or compress a spring that obeys Hooke’s law.

Hooke’s law states that the magnitude of force F on the spring and the resulting deformation ΔL are proportional, F = kΔL, where k is a constant.

So let’s go forward to obtain an expression for the potential energy of a spring. For our spring, we will replace ΔL (the amount of deformation produced by a force F) by the distance x that the spring is stretched or compressed along its length.

So the force needed to stretch the spring has magnitude F = kx, where k is the spring’s force constant.

derive an expression for the potential energy of an elastic stretched spring: Spring is at its initial position — Spring – initial position

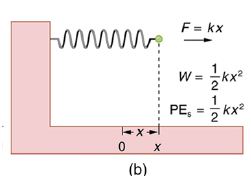
Derive an expression for the Potential Energy stored in a spring - the spring is stretched by a length x — Spring-with stretching

The force increases linearly from 0 at the start to kx in the fully stretched position.
The average force is kx/2.

Thus the work done in stretching or compressing the spring is Ws = Fd = force . displacement = (kx/2).x = (1/2)kx²

Thus we have completed the derivation of the expression for the Potential Energy stored in the spring.

Derive an expression for potential energy of a spring – Using Area under a graph of F versus x

Alternatively, we noted in Kinetic Energy and the Work-Energy Theorem that the area under a graph of F vs. x is the work done by the force. In Figure (c) we see that this area is also (1/2)kx² .

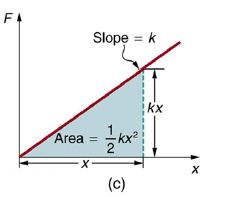
We, therefore, derive the equation of the potential energy of a spring, also known as the elastic potential energy as follows: PE=(1/2)kx²
where k is the spring’s force constant and x is the displacement from its undeformed position.

Summary | Take Away

We have derived an expression for the potential energy stored in the spring, also known as the elastic potential energy. We have shown 2 different ways to derive the equation. Here are a few points to remember.

– The elastic potential energy represents the work done on the spring and the energy stored in it as a result of stretching or compressing it by a distance of x.

– The potential energy of the spring does not depend on the path taken; it depends only on the stretch or compression x in the final configuration.

Related Study: Equation of time period for the mass-spring system with horizontal oscillation with derivation