Numerical problems on the first law of thermodynamics

Last updated on February 23rd, 2022 at 02:34 pm

In this post, we will solve a few numerical problems using the First Law of Thermodynamics.

Numerical problems on first law of thermodynamics

Question number 1)

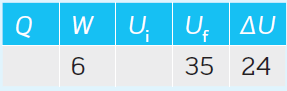
Complete the values in Table 1 (all values are in kJ).

Note that: W = 6 kJ is the work done on the system.

Solution:

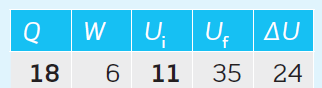
As per the data given in Table 1:
W_{on the system} = 6 kJ,
U_f = 35 kJ,
ΔU = 24 kJ

Q = ?
U_i = ?

The First Law of Thermodynamics is expressed generally as:
Q= ΔU + W (here +ive Q means heat is supplied and +ive W means work is done by the system)

And, here work is done on the system, & we will use the negative sign for work done on the system.
Q = ΔU – W_{on the system} …. (1)
=> ΔU = Q + W_{on the system} … (2)

Using equation (1)
Q = ΔU – W_{on the system} = 24 – 6 = 18 kJ …… (1)

Again, ΔU = U_f − U_i
=> U_i = U_f – ΔU = 35 – 24 = 11 kJ ………. (2)

Question number 2)

A foam cup is filled with hot water and allowed to cool while being stirred by a paddlewheel.
Initially, the water has an internal energy of 200 kJ, and while cooling it loses 150 kJ of heat.
The paddlewheel does 25 kJ of work on the water.

a) Calculate the change in the internal energy of the water.
b) Calculate the final internal energy of the water.

Solution:

Known values:
Ui = 200 kJ
W_{on the system} = 25 kJ
Heat transferred = Q =150 kJ

[The First Law of Thermodynamics is expressed generally as:
Q= ΔU + W (here +ive Q means heat is supplied and +ive W means work is done by the system)

And, here work is done on the system, & we will use the negative sign for work done on the system.
And, as Energy is lost, we will use the negative sign for Q as well. So the equation becomes:
– Q = ΔU – W_{on the system} …. (1)
=> ΔU = – Q + W_{on the system} … (2)]

a) Calculating ΔU :
ΔU = – Q + W_{on the system}
= (− 150 ) + (25)
= − 125 kJ
The change in the internal energy of the water is – 125 kJ. The negative sign means it has lost 125 kJ.

b) Calculating U_f :

ΔU = U_f − U_i

U_f = ΔU + U_i = -125 + 200 = 75 kJ

The final internal energy of the water is 75 kJ.

Question number 3)

A pump full of compressed gas is allowed to expand and 80 kJ of work is done by the gas on an object in the lab. At the same time, the gas is warmed by the addition of 100 kJ of heat energy. If the initial internal energy of the gas is 500 kJ, calculate the final internal energy.

Solution:

Known values:
U_i= 500 kJ
W_{by the system} = 80 kJ
Q = +100 kJ

[The First Law of Thermodynamics is expressed generally as:
Q= ΔU + W (here +ive Q means heat is supplied and +ive W means work is done by the system)

And, here work is done by the system, so,
Q = ΔU + W_{by the system} …. (1)
=> ΔU = Q – W_{by the system} … (2)]

a) Calculate ΔU :

ΔU = + 100 − 80
ΔU = + 20 kJ
The positive sign means it has gained 20 kJ.

b) Calculate U_f :
ΔU = U_f − U_i

=> U_f = ΔU + U_i
U_f= +20 + 500
= + 520 kJ
The final internal energy is +520 kJ.