Thermodynamic energy model & First law of thermodynamics

Last updated on January 6th, 2022 at 05:51 pm

In this post, we will draw the Thermodynamic energy model to relate heat in, work done on the system, heat out, and work done by the system. Before that, we will discuss the example of a bike pump and mention the First law of thermodynamics.

---

Heating up a Bike pump by increasing its internal energy – how?

We defined internal energy as the sum of the microscopic kinetic and potential energies of all the particles.

In this section, with an example, we will look at how internal energy can be changed.

When we pump up the tyres on a bicycle or pump up a ball, the bike pump gets hot. It seems that compressing the air inside a pump causes heating. Our arm muscles do work on the gas and the gas heats up. If we leave the same pump lying in sunlight it also gets hot. Heat energy from the Sun is transferred into the gas and heats it up.

Pumping up a ball makes the pump hot. The pump also gets hot if it is left in the Sun.

So, we can heat the pump up in two ways: by doing work on it and by adding heat.

Does that mean heat and work are interchangeable? That is, can one form of energy be transformed into the other because they both change internal energy (as measured by the temperature)?

If the pump feels hot, how do we know if it was heated by work done on it by your muscles, or by the Sun? We can’t tell – the path by which the pump gets hot is unknown, and we can’t tell unless we see what happened beforehand.

Interpretation of the First law of thermodynamics

We can develop a relationship between heat, work, and internal energy.

Firstly, we should call the bike pump the ‘system’ so that we can generalize later.

The internal energy of the gas in the pump (the system) has increased because it is hotter – but this could have come from heat
added from a high-temperature source (the Sun), or by work done by your muscles on the system.

Either way, it results in higher internal energy for the gas inside.

When work is done on the system
To the initial amount of internal energy in the system, U_i, we can add the net amount of heat, Q, and the net amount of work done on the system, W, which gives us the final internal energy, U_f.
This can be stated as: U_i + Q + W = U_f.
This equation can be rearranged to: U_f – U_i = Q + W……………. (1)
Now, By letting, U_f – U_i = ΔU
ΔU = Q + W……………. (2) [here W is the work done on the system]

When work is done by the system
If the system does work (W) on the surroundings, then we get a different set of equations:
In this case, when the system does work W on the surroundings, then we can write U_i + Q – W = U_f
=> U_f – U_i = Q – W …………… (1.1)
=> ΔU = Q – W ……….. (2.1)

We can summarise this as: The change in internal energy of a system is equal to the energy added or removed by heating plus the work done on or by the system.

This is an interpretation of the first law of thermodynamics.

Also read: Statement and formulas of the first law of thermodynamics

This conservation law states that the total energy of a system remains constant; energy can neither be created nor destroyed, rather, it transforms from one form to another.

Thermodynamic energy model

In the case of the bicycle pump mentioned earlier, the internal energy (thermal energy) of the system (the bike pump) was increased by adding heat to it (from the Sun) or by doing work on it (using your muscles).

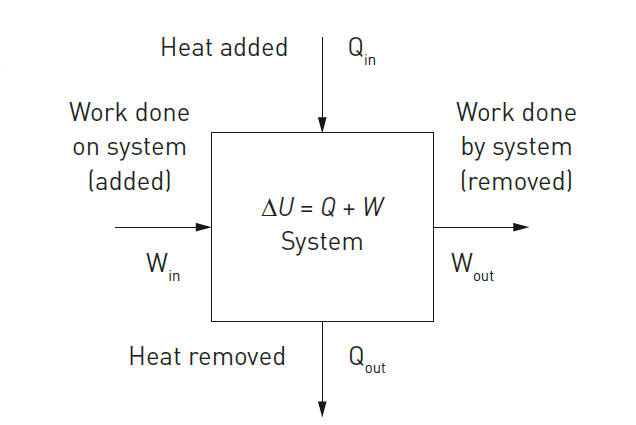
The diagram in Figure 1 is called the thermodynamic energy model as it shows the two inputs (heat in, and work done on the system) and the two outputs (heat out, and work done by the system).

Conventions in the thermodynamic energy model

Q_in, Q_out, W_in, W_out are all positive and the in/out arrows show direction.
• Q_net (or Q) = Q_in – Q_out.
• W_net (or W) =W_in – W_out.
• If Q positive, there is net heat in (added).
• If Q is negative, there is net heat out (removed).
• If W is positive, there is net work in (done on the system).
• If W is negative, there is net work out (done by the system).
We can represent the net energy quantities as follows:
Net heat energy is Q_net (or just Q) = Q_in – Q_out
Net work is W_net (or just W) = W_in – W_out