Electromagnetic Induction – Revision Notes
Last updated on December 15th, 2023 at 11:42 am
In this post, we explore electromagnetic induction – the creation of an electric current from a changing magnetic field.
Whether the primary source of energy is burning coal, falling water, nuclear fission, or the Sun, virtually all of the electricity generated in the world’s power stations is the result of electromagnetic induction. Electromagnetic induction is one of nature’s fundamental principles.
- Electromagnetic Induction – Revision Notes
- Electromagnetic Induction: Experimental Observations
- Observations – in a nutshell
- Magnetic Flux – definition & equation
- Magnetic Field strength depends on the closeness or density of lines of force
- Magnetic flux in terms of magnetic field lines
- Magnetic Field strength is magnetic flux density
- Units of magnetic flux
- Units of the magnetic field in terms of flux density
- Equation of induced current in a coil due to electromagnetic induction
Electromagnetic Induction – Revision Notes
In 1831, Englishman Michael Faraday and American Joseph Henry independently discovered how to create an electric current by using magnetism. And this was the beginning of a massive expansion in our understanding and use of electricity. It became clear that it would be possible to produce electricity in quantities far beyond the capacities of chemical batteries.
After Oersted’s discovery that an electric current produces a magnetic field, Michael Faraday was convinced that somehow a magnetic field should be able to produce an electric current.
He soon found that any method of changing the amount of magnetic field cutting through a coil of wire created a small current in the wire, but only while it was changing. You may read about Faraday’s law of electromagnetic induction here.
Simply moving a permanent magnet into a coil induced a brief current pulse, with another brief pulse in the opposite direction when it was removed.
The creation of an electric current in a loop of wire due to changes in a magnetic field is called electromagnetic induction.
Know about the Magnitude and direction of Induced emf
Electromagnetic Induction: Experimental Observations
We can gain a feel for electromagnetic induction by experimenting with a coil of wire near a permanent magnet or an electromagnet. The coil is connected to a galvanometer – a sensitive current meter.
Note: We use the term ‘loop’ for a single closed conducting path, such as a circle of wire, and the term ‘coil’ for a series of loops wound together.
Experimental observation 1 – with a moving magnet
If the magnet is moved towards the coil, the galvanometer registers a current, but only while the magnet is moving, not once it stops.
If the magnet is moved away, a current in the opposite direction is registered.
In fact, it does not matter whether it is the coil or the magnet that is in motion – it is only the relative motion that is important.
Experimental observation 2 – with stationary electromagnet
Next, we use a stationary electromagnet but change the field by turning it on and off.
When the current in the electromagnet is switched on, there is a brief pulse of current through the galvanometer, indicating an induced current in the coil as the magnetic field increases.
While a steady current flows in the electromagnet no current is registered by the galvanometer.
When the electromagnet is turned off again, the galvanometer indicates another brief pulse of current in the coil, this time in the opposite direction.
If we increase or decrease the current in the electromagnet (i.e. if we change the strength of the field) the galvanometer again registers a small current. Read more about electromagnetic induction experiments.
Observations – in a nutshell
So it seems that any method of changing the ‘amount’ of magnetic field cutting through the coil will induce a current.
Indeed, even changing the shape of the coil so that more or less field passes through it results in an induced current.
In all cases, the larger the change and the faster the change, the greater the current.
Magnetic Flux – definition & equation
To describe the ‘amount of field’ more precisely, physicists use a quantity called magnetic flux (ΦB).
Magnetic flux (ΦB) is defined as the product of the magnetic field, B, and area A⊥. A⊥ is the effective area of the loop perpendicular to the field lines.
(If the loop is not perpendicular to the field, A⊥ will equal Acosθ, where θ is the angle between the field and the normal to the coil.)
Magnetic flux equation is given by: ΦB = BA⊥ = BA cosθ
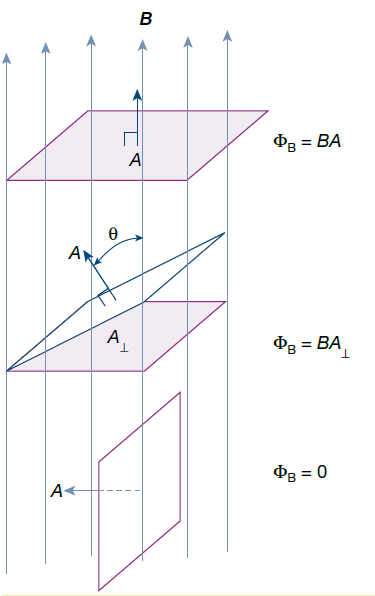
( A⊥ here is shown shaded)
Magnetic Field strength depends on the closeness or density of lines of force
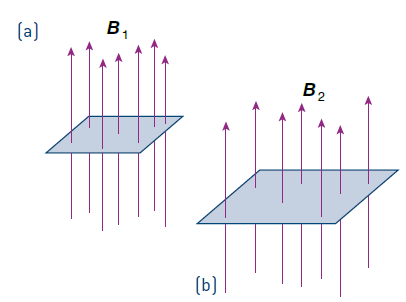
Faraday pictured a magnetic field represented by many lines of force, the closeness of the lines representing the strength of the field. Where the lines are crowded (near the poles of a bar magnet, for example) the field is strong; where they are less dense the field is weaker.
Magnetic flux in terms of magnetic field lines
Magnetic flux is actually like the total number of lines of force of a magnetic field – hence, the same flux could be produced by a weak field spread over a large area (the lines are spread out) or a strong field concentrated in a small area (a high density of lines).
Magnetic Field strength is magnetic flux density
This picture below leads to the common expression for the strength of the magnetic field, B, as the magnetic flux density.
So, the strength of the magnetic field, B = ΦB / A⊥
B can be thought of as proportional to the number of lines of force passing through a unit of area perpendicular to the lines.
Units of magnetic flux
Thus, the unit of magnetic flux is the magnetic field unit (Tesla) multiplied by area (m2) or T m2.
This unit is also known as the Weber (1 Wb = 1 T m2).
Units of the magnetic field in terms of flux density
Conversely, this implies that the unit for the magnetic field can be expressed as the flux density, or Weber per square meter (Wb/m2), a unit that is still often used.
Equation of induced current in a coil due to electromagnetic induction
Faraday went on to show that the amount of induced current in a coil was proportional to the rate at which the number of lines of force cutting through a coil was changing; that is, the rate of change of magnetic flux passing through the coil.
The induced current in a conducting loop is proportional to the rate of change of flux:
I ∝ ΔΦB / Δt
