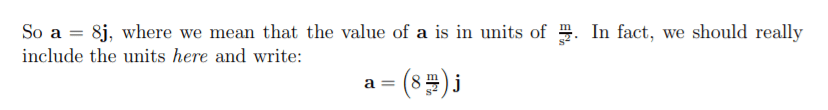Motion in 2 and 3 Dimensions – formula & numerical

Last updated on February 8th, 2024 at 10:40 am

We will discuss and list down the formulae of position, velocity, and acceleration related to the Motion in two and three Dimensions using unit vectors i, j, and k format.

We will list down the 2-Dimensional equivalent of motion equations or suvat equations. Also, we will solve numerical problems using the formulas of the position vector, velocity vector, and acceleration vector in 2 Dimension and 3 Dimension.

---

Position formula (in 3 dimensions)

In three dimensions, the location of a particle is specified by its location vector, r:
r = x i + y j + z k

If during a time interval ∆t the position vector of the particle changes from r1 to r2, the displacement ∆r for that time interval is represented as: ∆r = r1 − r2
= (x2 − x1)i + (y2 − y1)j + (z2 − z1)k
∆r= (∆x) i + (∆y) j + (∆z) k

Velocity formulae (in 3 dimensions)

Average velocity formula in 3 dimensions

If a particle moves through a displacement ∆r in a time interval ∆t then its average velocity for that interval is:
v =∆r/∆t =(∆x/∆t) i + (∆y/∆t) j + (∆z/∆t) k

Instantaneous velocity formula in 3 dimensions

A more interesting quantity is the instantaneous velocity v, which is the limit of the average velocity when we shrink the time interval ∆t to zero.

Instantaneous velocity is the time derivative of the position vector r:
v =dr/dt = d(xi + yj + zk)/dt= (dx/dt) i +(dy/dt) j +(dz/dt) k
This Instantaneous velocity can be written as:
v = v_xi + v_yj + v_zk
where v_x = (dx/dt) v_y =(dy/dt) v_z =(dz/dt)

Acceleration formulae (in 3 dimensions)

Average acceleration formula in 3 dimensions

If a particle’s velocity changes by ∆v in a time period ∆t, the average acceleration a for that period is
a =∆v/∆t = ∆(v_xi +v_yj + v_zk)/∆t = (∆v_x/∆t)i +(∆v_y/∆t) j + (∆v_z/∆t)k

Instantaneous acceleration formula in 3 dimensions

But a much more interesting quantity is the result of shrinking the period ∆t to zero, which gives us the instantaneous acceleration, a. It is the time derivative of the velocity vector v:
a =dv/dt=d(v_xi +v_yj + v_zk)/dt = (dv_x/dt)i +(dv_y/dt)j + (dv_z/dt)k
which can be written: a = a_xi + a_yj + a_zk

where
a_x =dv_x/dt=d²x/dt²
a_y =dv_y/dt=d²y/dt²
a_z =dv_z/dt =d²z/dt²

2 dimensional Motion equations in vector format with Constant Acceleration

2-D motion equations – Let’s talk about the Motion equations in 2 dimensions when we have Constant Acceleration in Two Dimensions.

When the acceleration a (for motion in two dimensions) is constant we have two sets of equations to describe the x and y coordinates, each of which is similar to the suvat equations.

In the following discussion, the motion of the particle begins at t = 0.

The initial position of the particle is given by r₀ = x₀i + y₀j
and its initial velocity is given by v₀ = v_0xi + v_0yj
and the acceleration vector a = a_xi + a_yj is constant.

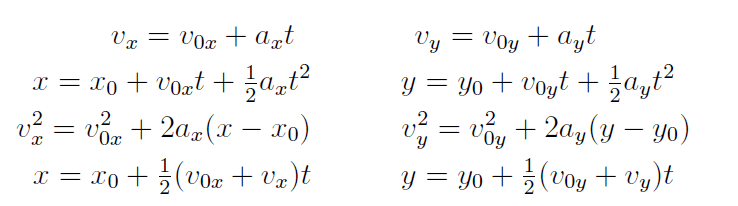
Worked Examples | Solved Numerical problems

Let’s solve a few selected numerical problems on Motion in 2 and 3 Dimensions using the formulae of the position vector, velocity vector, and acceleration vector in 2 Dimensions.

1. The position of an electron is given by r = 3.0t i − 4.0t^2 j + 2.0 k (where t is in seconds and the coefficients have the proper units for r to be in meters).
   (a)What is v(t) for the electron? (b) In unit–vector notation, what is v at t = 2.0 s?
   (c) What are the magnitude and direction of v just then?
   
   Solution:

2. A particle moves so that its position as a function of time in SI units is r = i + 4t^2 j + t k. Write expressions for (a) its velocity and (b) its acceleration as functions of time.
   
   Solution: