The gas laws | Statement, Formula, graph of Charles’ law, Boyle’s Law & Pressure law

Last updated on October 23rd, 2021 at 12:38 pm

The gas laws tell us the relationship between pressure, temperature, and volume of gases. The gas laws can be stated in a convenient form for calculations when absolute temperatures are used. The laws we are going to cover here are (1) Charles’ Law (2) Pressure Law, and (3) Boyle’s Law.

Charles’ law | Statement of Charles’ law with explanation

Charles’ law may be stated as follows: The volume of a fixed mass of gas is directly proportional to its absolute temperature if the pressure is kept constant.

We can then say that the volume V is directly proportional to the absolute temperature T, i.e. doubling T doubles V, etc. Therefore
V ∝ T or V = constant × T
or
V/T = constant

Use this formula to solve numerical problems based on Charles’ law.

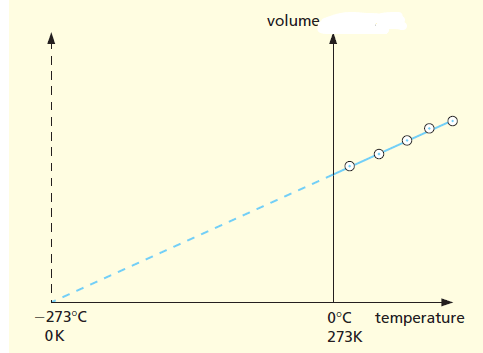
Charles’ law Graph from the lab experiment

Let’s have a quick view of Charles’ law Graph to understand the effect of temperature on volume with pressure constant.

The graph does not pass through the Celsius temperature origin (0 ºC). If they are produced backward they cut the temperature axis at about –273 ºC. This means at 0 ºC the volume of the gas is non-zero, but at –273 ºC the volume of the gas touches the zero mark.

This temperature (–273 ºC) is called absolute zero because it is found to be the lowest temperature possible. It is the zero of the absolute or Kelvin scale of temperature. Degrees on this scale are called kelvins and are denoted by K.

Alternate presentation of Charles’ law

Charles’ law states that, at constant pressure, the volume of a given mass of a gas increases or decreases by 1/273 of its volume at 0°C for each one degree rise or fall in temperature.

Let V₀ be the volume of a given mass of a gas at 0°C and V_t is its volume at any temperature t°C, then the volume, V_t may be written in terms of Charles’ law (at constant pressure) as :

For 1 degree rise in temperature, volume increases = V₀ x (1/273)

For t degree rise in temperature, volume increases = V₀ x (1/273) x t

∴ Volume at t°C, V_t = Initial volume + Increase in volume = V₀ + V₀ x (1/273) x t

V_t = V₀ ( 1 + t/273)

Pressure Law Statement | Gay Lussac’s law

Gay Lussac’s law or Pressure law gives Pressure temp relationship.

The pressure law or Gay Lussac’s law may be stated as follows: The pressure of a fixed mass of gas is directly proportional to its absolute temperature if the volume is kept constant.

As per Pressure Law, pressure p is directly proportional to the absolute temperature T.
p ∝ T or p = constant × T
or
p/T = constant

Physical significance of Gay Lussac’s law or pressure law

Pressure in well-inflated tyres of automobiles is almost constant. But on a hot summer day, this increases considerably and the tyre may burst if pressure is not adjusted properly. Similarly, during winters, on a cold morning, we find the pressure in the tyres of a vehicle decreased considerably.

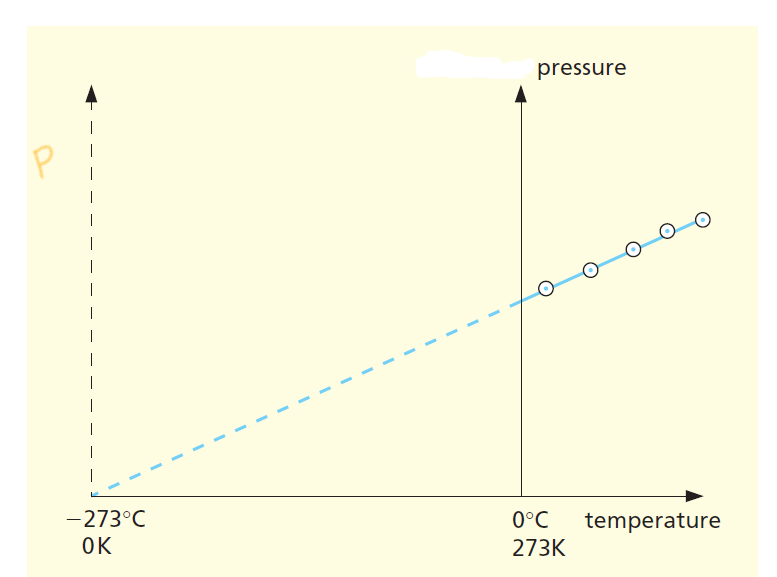
Pressure Law Graph

Here is the Pressure law graph.

Boyle’s Law Statement | explanation

Boyle’s law may be stated as follows: The pressure of a fixed mass of gas is inversely proportional to its volume if its temperature is kept constant.

p is inversely proportional to V.
In symbols: p ∝ 1/V
p = constant x (1/V)
∴ pV = constant
If several pairs of readings, p₁ and V₁, p₂ and V₂, etc. are taken, then it can be confirmed that p₁V₁ = p₂V₂ = constant.

Use this formula to solve numerical problems based on Boyles’ law.

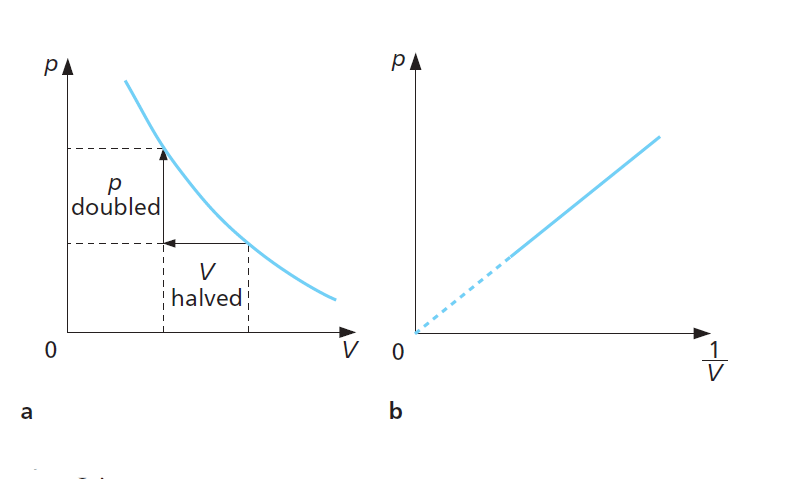
Boyle’s Law graphs

Since p is inversely proportional to V, then p is directly proportional to 1/V. A graph of p against 1/V is, therefore, a straight line through the origin.

Combining the Gas Laws

The three equations can be combined giving the following equation:
pV/T = constant

For cases in which p, V, and T all change from, say, from p₁, V₁, T1 to p2, V₂, T₂, then
p₁V₁ / T₁= p₂V₂/ T₂

Numerical Problems – How to use the gas Laws to solve numericals

Here we will see how to use the gas laws to solve numerical problems. We need to follow the rules listed below.

1. All temperatures must be in K.
2. Any units can be used for p and V provided the same units are used on both sides of the equation.
3. In some calculations, the volume of the gas has to be found at standard temperature and pressure, or ‘s.t.p.’. This is temperature 0 ºC and pressure 1 atmosphere (1 atm = 105 Pa).

solve a numerical using the gas laws

Question: A bicycle pump contains 50 cm3 of air at 17 ºC and at 1.0 atmosphere pressure. Find the pressure when the air is compressed to 10 cm3 and its temperature rises to 27 ºC.

Solution:
p1 = 1.0 atm p2 = ?
V1 = 50 cm3 V2 = 10 cm3
T1 = 273 + 17 = 290 K T2 = 273 + 27 = 300 K

We will use this equation to solve this: p₁V₁ / T₁= p₂V₂/ T₂
p₂ = (p₁V₁ T₂ ) / (T₁ V₂ ) = (1x 50×300)/(10×290) = 5.2 atm