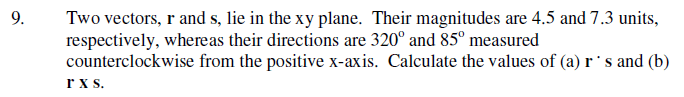Numerical problems Vector Physics (Class 11 & Class 12)

Last updated on July 5th, 2023 at 04:19 am

This post presents Numerical problems in Vector Physics. These 2 worksheets will help students who are preparing for Class 11 Physics for different boards like IGCSE, GCSE, ISC, CBSE, etc. Also covers the syllabus of many international boards for HSC grades 11 & 12.

This is equally helpful for those students who are focusing on competitive examinations like AP Physics, IIT JEE mains, and similar other exams to test their preparedness. These numerical sets contain medium to hard problems from the Vector chapter of high school physics.

Numerical problems Vector Physics (solved) – Set 1

Q1)
A sailing boat is kept motionless in a fast-flowing river by ropes held by two boys, A and B, on opposite banks as shown in the diagram below. The water exerts a force of 450 N (parallel to the bank) on the boat. The angles of the ropes connecting A and B with the boat, with respect to the river bank, are 55° at A and 35° at B as shown in the diagram below.

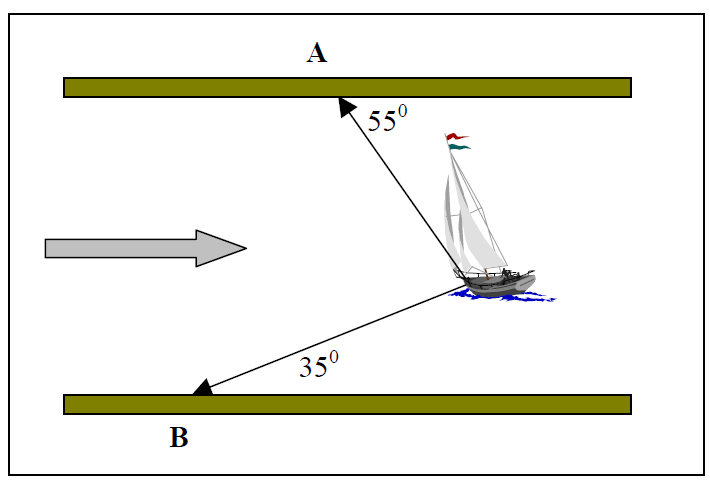
a) Give a reason why it is correct to say that the forces acting on the boat are in equilibrium.
b) Draw a fully labeled diagram of forces indicating all the forces acting on the boat.
c) Determine the magnitude of the forces acting on the boat.

Solution(hints):

a) The boat is at rest/stationary. According to Newton’s 1st law: as no resultant force acting on the boat, the boat is at rest/stationary.
b)

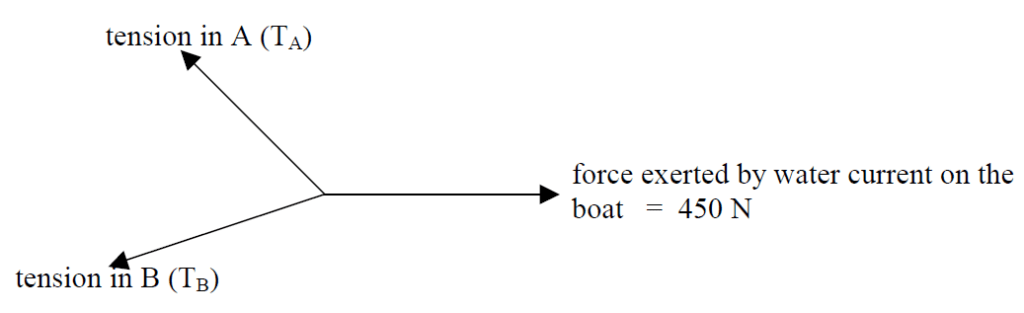
c) Ta cos 55 + Tb cos 35 = 450
Ta sin 55 = Tb sin 35
Solve these 2 equations to get Ta and Tb.

Q2)
A freighter is 240 km due east of a harbor. A current is flowing due south and the freighter captain wishes to set a course so that he can reach the harbor directly. He sets the course at 22.6° north of west and sets a speed through the water of 13 km/h and the freighter eventually reaches the harbor in 20 hours.

a) Define the RESULTANT of two vectors.
b) Calculate the resultant velocity of the freighter.
c) Draw a velocity vector diagram indicating the velocity of the current v_c, the velocity of the freighter through the water v_f, and the resultant velocity of the freighter v_r, showing how they are related.
d) Determine the velocity of the current.

Q3)
A bricklayer on top of a building runs short of bricks. He lowers a bucket on a cable to a worker on a truck. The worker pulls the bucket horizontally to the right to bring it close to the truck.

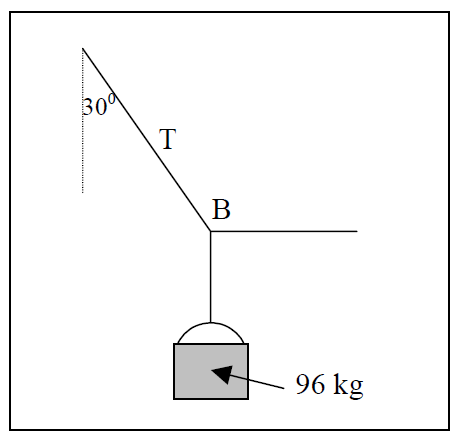
The worker holds the bucket stationary so that it makes an angle of 30° to the vertical (as shown in the diagram). Another worker then fills the bucket with bricks until the total mass of the bucket is 96 kg.

a) What is the weight of the bucket?
b) Are the forces acting on the bucket in equilibrium? Explain.
c) Draw a fully labeled force diagram (not to scale) showing all the forces acting on the bucket. (Represent the bucket with a large dot.)
d) Draw a labeled vector diagram showing the relationship between the forces.
e) Determine the horizontal force exerted on the bucket by the worker to hold it in place
f) Determine the tension in cable T. You can use a scale diagram (scale: 10 mm = 100 N) or trigonometry.

Q4)
An electric lamp of mass 0.8 kg is attached by an electric cable to the ceiling at point D.

To position it directly over her desk, Tito has pulled the lamp to one side by a string tied to the lamp holder H and fixed it to point E on the ceiling.

Tito is curious as to whether the tension in the electric cable is affected when the lamp is pulled aside. To investigate this, she measures the angles which the cable and the string make with the ceiling and finds them to be 60° and 40° respectively as shown in the diagram at the right.

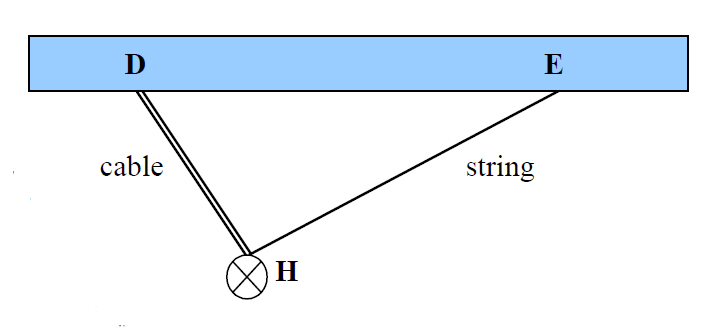
a) What would be the tension in the electric cable if the lamp were hanging down straight?
b) Draw a force diagram for the lamp holder H and label all the forces acting on it.
c) Find the tensions in the electric cable and the string either by calculation or by accurate scale drawing.
d) Has the tension in the electric cable been affected when the lamp is pulled aside?

Q5)
Two forces act over pulleys to support a block of wood as shown in the diagram below.

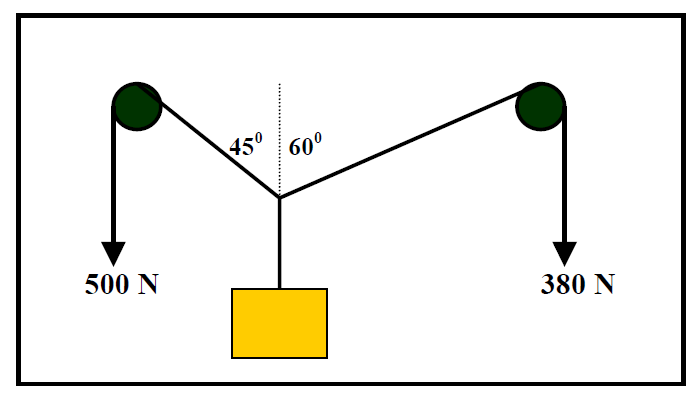
Calculate:

1. The vertical component of each force acting on the object.
2. The resultant vertical force acting on the object.
3. The weight of the block.

Numerical problems on Vector Physics – worksheet set 2