Derive the relation between Current and Drift Velocity
Last updated on May 29th, 2023 at 05:21 am
Here we will derive the equation showing the relationship between current and drift velocity. The drift velocity is the average velocity of the free charges and it is in the direction opposite to the electric field for electrons.
Drift velocity is quite small since there are so many free charges. If we have an estimate of the density of free electrons in a conductor, we can calculate the drift velocity for a given current. The larger the density, the lower the velocity required for a given current.
Relation between current and drift velocity
The equation that describes the relationship between the current (I) in a conductor and the drift velocity (v) is as follows:
I = nAve
where A = area of cross-section of the conductor, n = number of charge carriers (electrons) per cubic meter, e = charge on each charge carrier(electron), and v = drift velocity of charge carrier electron.
Derive the relationship between Current and drift velocity | Derivation of the relation between Current and Drift Velocity
For a conductor, the current I is given by:
I = nAvq
where A = area of cross-section of the conductor, n = number of charge carriers per cubic meter, q = charge on each charge carrier, and v = drift velocity of charge carriers.
Note: When the charge carrier is electron, then the above equation becomes I = nAve
e=charge of an electron.
Let’s derive the equation that represents the relation between current and drift velocity.
This equation may be deduced as follows, with reference to Figure (a) given below:
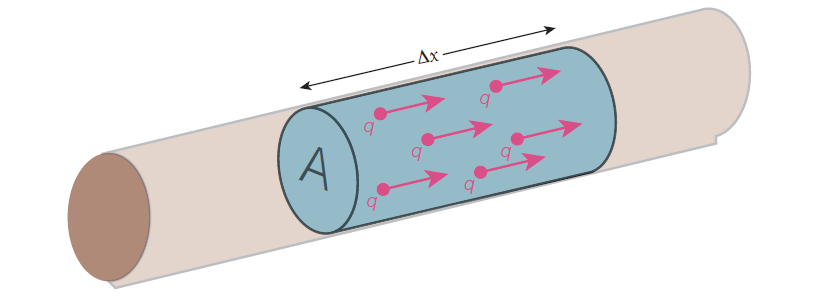
Consider a section of wire of length Δx
The volume of wire in this section will be ΔV = AΔx
If there are n charge carriers per unit volume in the wire, the number in volume ΔV will be
ΔN = nΔV = nAΔx
If the charge on each charge carrier is q, the quantity of charge within the section will be
ΔQ = nAqΔx
Suppose each charge carrier takes a time Δt to travel the distance Δx.
Dividing both sides of the equation by Δt gives us
ΔQ/Δt = nAq Δx/Δt
But ΔQ/Δt = I and Δx/Δt = v
Hence I = nAvq
So this is the equation describing the relationship between current (I) and the drift velocity (v).
When the charge carrier is an electron this equation can be rewritten as follows:
I = nAve,
where e is the charge of an electron
As you have derived the current & drift velocity equation, now it’s time to solve a few numerical problems using this formula. Here is the post you must visit to solve some selected problems.
Related Reading:
Solve numerical problems using the current-drift velocity equation
How Small drift speed of electron causes high-speed electric current?
