How to Calculate the Mechanical Advantage of Wheel and Axle?
Last updated on May 18th, 2023 at 03:04 pm
Mechanical Advantage of Wheel and Axle = M.A = Radius of the wheel/radius of the axle = R/r.
As R > r, the MA of the wheel and axle is always greater than 1.
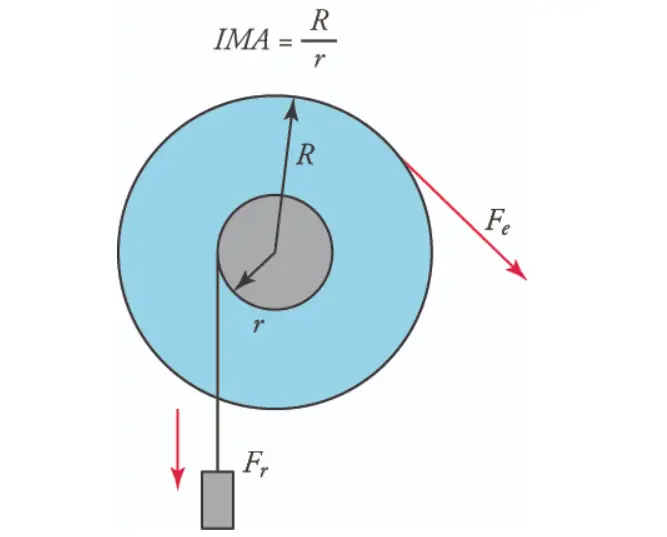
The wheel and axle are actually a form of lever. The difference is that the effort arm can rotate in a complete circle around the fulcrum, which is the center of the axle.
The force applied to the outside of the wheel causes a greater force to be applied to the rope that is wrapped around the axle.
As shown in the figure, the ideal mechanical advantage is calculated by dividing the radius of the wheel by the radius of the axle.
Any crank-operated device is an example of a wheel and axle.
In this post, we will see how to calculate the mechanical advantage of the Wheel and Axle.
What is the ‘wheel and axle’?
The wheel and axle is a simple machine that consists of a wheel attached to a strong cylindrical axle.
The radius of the wheel (R) is greater than the radius of the cylindrical axle (r). The wheel and the axle have a common axis. When these two parts rotate together a force is transferred from one to the other.
The wheel and axle can be viewed as a version of the lever where a driving force or effort is applied tangentially to the perimeter of the wheel and a load force is applied to the axle.
To rotate the thin rod-like axle a force needs to be applied on the wider wheel fixed to the axle. A tangential force applied to the periphery of the large wheel can exert a larger force on a load attached to the axle, achieving a mechanical advantage.
Setting up a wheel and axle combination to find out the MA of this simple machine
A string is wound around the axle cylinder and a Load is attached to one free end of this string.
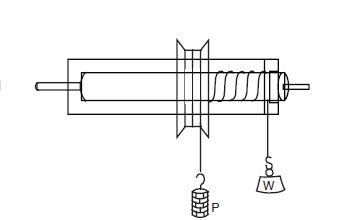
Now the other free of the string is taken and it’s wound around the wheel in such a way that the windings of the rope on the wheel are in the opposite direction to that of the windings on the axle.
An effort is applied to the free end of the string which is wound around the wheel.
Deriving the Mechanical Advantage formula for the wheel and axle
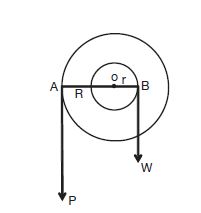
During rotational equilibrium conditions, the rotating effect of the wheel is equal to the rotating effect of the cylinder. (now see Figure 2 above)
⇒ Moment of the wheel about the axis = Moment of the axle about the axis
⇒ P × R = W × r, where P is the effort, and W is the load.
⇒ W/P = R/r
And, Mechanical Advantage =load/effort=W/P= R/r
Mechanical Advantage of Wheel and Axle = M.A =Radius of the wheel/radius of the axle
As R > r, the MA of the wheel and axle is always greater than 1.
Related Study
