Mechanical Advantage of an Inclined Plane with formula
Last updated on May 18th, 2023 at 02:44 pm
The mechanical advantage of an inclined plane is calculated as the ratio of the length of the incline and the height of the incline. It can also be calculated using the value of 1/(sin θ), where θ is the angle of inclination.
An inclined plane is a simple machine that makes our life easier. All sloping, paved surfaces for walking or driving are inclined planes.
But how to find out the Mechanical advantage (MA) of an inclined plane and what is its formula – this is what we will discuss here.
So let’s begin the derivation of the formula of the mechanical advantage of inclined planes.
How to find the Mechanical Advantage of the inclined plane?
Let’s consider a frictionless inclined plane (or incline). Say a mass is sliding down this incline from rest. The length of the incline is d and the height is h. θ is the angle of inclination. Let W be the load to be moved along the inclined plane by applying effort F.
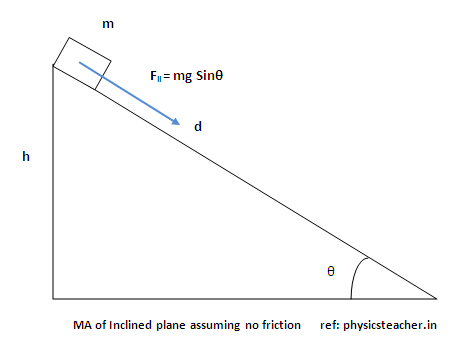
If the surface of the plane is considered to be frictionless, then the output work is equal to the input work, i.e., work done by the effort is equal to work done on the load.
⇒ F × d = W × h
⇒ W/F = d/h ……………….. (1)
This is the expression of mechanical advantage. So we have to find out this ratio d/h to find out the mechanical advantage of the inclined plane.
Mechanical Advantage formula of Inclined plane in terms of the angle of inclination θ
We already know that the force parallel to the incline is given by F|| = mg sinθ. [ see how here: inclined plane].
Note that this F|| is the component of gravity that acts parallel to the incline. (see the image)

The work done by F|| (the component of gravity parallel to the incline) is given by:
W|| = (mg sin θ)(d) = mgd sin θ …… (2)
If the mass m were dropped from the height h, the work done by gravity (directly) would be
Wg = mgh …… (3)
In the absence of friction, the work done by both of these paths would be equal:
W|| = Wg
=> mgd sin θ = mgh
Hence,
h = d sin θ …… (4)
Here from Equation 1 & Equation 4, we can see that:
MA= d/h = 1/(sin θ) …………….(5)
This is the expression of the mechanical advantage of an inclined plane.
Analysis of the MA formula of inclined planes
θ being less than 90 degrees in an inclined plane, sin θ is always less than 1.
This clearly shows from (5) that d/h > 1 ……………….. (6)
From (6) it clearly shows that following the incline needs traversal of more distance, that is more displacement happens along the incline compared to the direct or vertical change of height.
Now as the ‘work done‘ is the product of force and displacement in the direction of the force and the work done is the same in both the cases we are considering, we can easily say that the force required along the incline is less than the gravity.
In brief: In this ideal situation, the force given by gravity (mg) is greater than the force parallel to the incline (mg sin θ). However, the length of the incline is proportionally larger than the height. Thus, while the ‘work done’ is the same, the force can be reduced at the expense of distance. This is the essence of a simple machine.
If we reverse the process (push the object up the ramp), we can see the advantage of this machine.
We can apply less effort (force) to do the same work as lifting the object to the height of h if we compensate by going a longer distance. The height h is considered the resistance distance that must be moved through against the force of gravity.
Ideal Mechanical Advantage (IMA) of the inclined plane
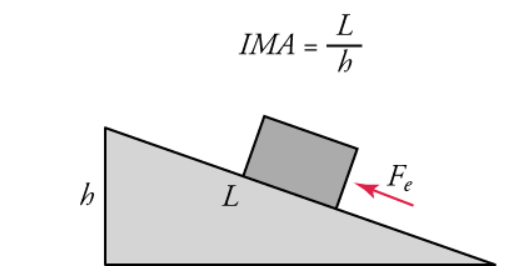
The Ideal Mechanical Advantage (IMA) is defined as follows:
IMA = Effort distance/resistance distance = length of incline/height of the incline
For example, if the IMA of a ramp is equal to 4 (length is four times as long as the height), then under ideal conditions (no friction) we can use one-fourth the weight of the object as effort when pushing it up the ramp (as long as we go four times as far).
Real Mechanical Advantage (RMA) of the inclined plane
If there is friction, the IMA does not change, but we would need to use more effort to overcome friction. The real mechanical advantage would be defined as the ratio of resistance force (in this case, the weight) to the actual effort force used:
RMA = resistance force/ actual effort force
Summary | The formula of MA of an inclined plane
Ideal Mechanical Advantage = IMA = Effort distance/resistance distance = length of incline/height of incline = 1 / Sin θ [where θ is the angle of inclination]
Real Mechanical Advantage = RMA = resistance force/ actual effort force
Relevant study
MA of Lever
