What is the principle of moments and how to use it to solve numerical problems?

Last updated on April 14th, 2021 at 04:37 pm

Here we will state the principle of moments first and then will see how to use it to solve numerical physics problems related to equilibrium.

What is the principle of moments?

The Principle of Moments states that the rotational equilibrium of a body is possible only when the sum of clockwise moments is equal to the sum of anti-clockwise moments acting on that body.

How to Solve numerical problems on rotational equilibrium with the principle of moments?

Let’s solve one numerical problem by applying the principle of moments.

1 ] The beam shown in the figure is 2 m long and has a weight of 20 N. It is pivoted as shown. Two forces of 20 N and 10 N are acting on it as shown in the figure. What force F must be applied downwards at the other end (see the figure for force F) to balance the beam? The pivot point is shown as the red triangle.

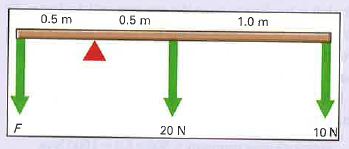
Solution:

Both 20 N and 10N forces are creating clockwise moments. And the sum of clockwise moments is = (10×1.5 + 20×0.5) Nm = (15 + 10) Nm = 25 Nm…. (1)

And the anticlockwise moment created by the force F Newton = F x 0.5 Nm …(2)

For equilibrium, clockwise moment must be equal to anticlockwise moment.

Hence, as per principle of moments, from equation (1) and (2):

F x 0.5 = 25
=> F = 25/0.5 N = 50 N
Answer: 50 N