Bernoulli’s Equation with Derivation
Last updated on June 24th, 2023 at 05:04 pm
Bernoulli’s equation describes the relationship between pressure and velocity in fluids quantitatively. Hence, this equation is named after its discoverer, the Swiss scientist Daniel Bernoulli (1700–1782).
Bernoulli’s equation states that for an incompressible, frictionless fluid, the following sum is constant: P+(1/2)ρv2+ρgh=constant, where P is the absolute pressure, ρ is the fluid density, v is the velocity of the fluid, h is the height above some reference point, and g is the acceleration due to gravity.
If we follow a small volume of fluid along its path, various quantities in the sum of the above equation may change, but the total remains constant.
Let the subscripts 1 and 2 refer to any two points along the path that the bit of fluid follows;
Bernoulli’s equation becomes P1+(1/2)ρv12+ρgh1=P2+(1/2)ρv22+ρgh2
Bernoulli’s equation & the conservation of Energy principle
Bernoulli’s equation is a form of the conservation of energy principle. Note that the second and third terms are the kinetic and potential energy with m replaced by ρ. In fact, each term in the equation has units of energy per unit volume.
Here, (1/2)ρv2 is the kinetic energy per unit volume.
And, ρgh is the gravitational potential energy per unit volume.
Note that pressure P has units of energy per unit volume, too. Since P = F/A, its units are N/m2. If we multiply these by m/m, we obtain N ⋅ m/m3 = J/m3, or energy per unit volume.
Bernoulli’s equation is, in fact, just a convenient statement of conservation of energy for an incompressible fluid in the absence of friction.
Derivation of Bernoulli’s equation
We will apply the conservation of energy principle to derive Bernoulli’s equation.
At any point along the path that the bit of fluid follows, the total energy can be obtained by adding the pressure energy, kinetic energy, and gravitational potential energy at that point.
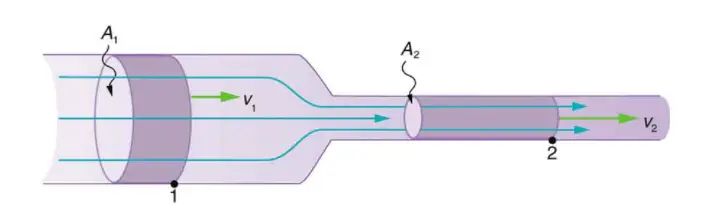
So at point 1 in the above diagram (figure 1), the total energy E1 = pressure energy at point 1 + kinetic energy at point 1 + gravitational potential energy at point 2.
Hence, E1 = P1 V + (½) m v12 + mgh1
Similarly, at point 2, the total energy E2 = P2 V + (½) m v22 + mgh2
By applying the conservation of energy principle:
E1 = E2
=> P1 V + (½) m v12 + mgh1 = P2 V + (½) m v22 + mgh2
=> V [ P1 + (½) ρ v12 + ρgh1 ] = V [ P2 + (½) ρ v22 + ρgh2]
=> P1 + (½) ρ v12 + ρgh1= P2 + (½) ρ v22 + ρgh2
Bernoulli’s Equation (derived)
P+(1/2)ρv2+ρgh=constant, where P is the absolute pressure, ρ is the fluid density, v is the velocity of the fluid, h is the height above some reference point, and g is the acceleration due to gravity.
Bernoulli’s Equation for Static Fluids
Let us first consider the very simple situation where the fluid is static—that is, v1 = v2 = 0. Bernoulli’s equation in that case is
P1 + ρgh1 = P2 + ρgh2.
Bernoulli’s Equation at Constant Depth
Another important situation is one in which the fluid moves but its depth is constant—that is, h1 = h2. Under that condition, Bernoulli’s equation becomes:
P1+(1/2)ρv12=P2+(1/2)ρv22
Sample Numerical problem on Bernoulli’s Principle with solution
Question: The speed of water in a hose increased from 1.96 m/s to 25.5 m/s going from the hose to the nozzle. Calculate the pressure in the hose, given that the absolute pressure in the nozzle is 1.0 × 105 N/m2 (atmospheric, as it must be) and assuming level, frictionless flow.
How to approach to solve this problem?
Level flow means constant depth, so Bernoulli’s principle applies. We use the subscript 1 for values in the hose and 2 for those in the nozzle. We are thus asked to find P1.
Solution
P1+(1/2)ρv12=P2+(1/2)ρv22
Solving Bernoulli’s principle for P1 yields
P1 = P2 + (1/2)ρv22− (1/2)ρv12 = P2 + (1/2)ρ(v22−v12)
Substituting known values,
P1=71.01×105 N/m2+(1/2)(103 kg/m3)[(25.5 m/s)2−(1.96 m/s)2]=4.24×105 N/m2
Related Posts
Reynolds number, significance, formula, sample numerical
The Equation of Continuity with Derivation & Streamlines of fluid flow
