The Equation of Continuity with derivation & Streamlines of fluid flow
Last updated on August 28th, 2021 at 08:51 am
In this post, we will discuss two topics related to fluid dynamics. These topics are Streamlines and the Equation of Continuity with derivation. This physics tutorial is apt for class 11 physics for ISC, CBSE, IGCSE, and other boards (grade 11 and 12 for international boards).
Streamlines
The path taken by a fluid particle under a steady (laminar) flow is called a streamline. The velocity of such particle at each point along its path is always tangent to the streamline, as shown in Figure 1.
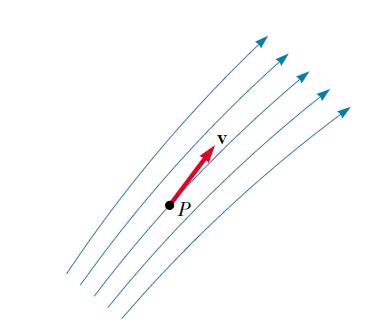
A set of streamlines like the ones shown in Figure 1 form a tube of flow. Note that fluid particles cannot flow into or out of the sides of this tube; if they could, then the streamlines would cross each other.
Equation of Continuity with derivation
Consider an ideal fluid flowing through a pipe of nonuniform size, as illustrated in Figure 2.
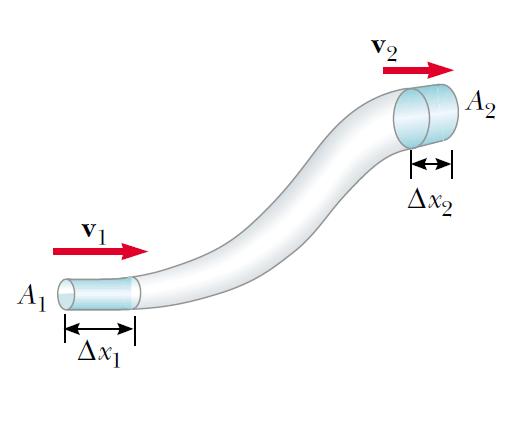
The particles in the fluid move along streamlines in a steady flow.
In a time t, the fluid with a speed v1 at the bottom end of the pipe moves a distance Δx1 =v1. t.
If A1 is the cross-sectional area in this region, then the mass of fluid contained in the left shaded region in figure 2 is
m1 = pA1 Δx1 = p A1 v1 t where p is the (nonchanging) density of the ideal fluid.
Similarly, the fluid that moves with speed v2 through the upper end of the pipe in the time t has a mass m2 = p A2 Δx2 =p A2 v2 t.
However, because mass is conserved and because the flow is steady, the mass that crosses A1 in a time t must equal the mass that crosses A2 in the time t.
That is, m1=m2,
or, pA1v1t= pA2v2t
=> this means that A1 v1=A2 v2 = constant
This expression A1 v1= A2 v2 = constant is called the equation of continuity.
It states that the product of the area and the fluid speed at all points along the pipe is a constant for an incompressible fluid.
This equation tells us that the speed is high where the tube is constricted (small A) and low where the tube is wide (large A). The product Av, which has the dimensions of volume per unit time, is called either the volume flux or the flow rate.
The condition Av=constant is equivalent to the statement that the volume of fluid that enters one end of a tube in a given time interval equals the volume leaving the other end of the tube in the same time interval if no leaks are present.
Statements of the Equation of Continuity
1) The Equation of Continuity states that the product of the area and the fluid speed at all points along the pipe is a constant for an incompressible fluid.
2) The Equation of Continuity states that the volume of fluid that enters one end of a tube in a given time interval equals the volume leaving the other end of the tube in the same time interval if no leaks are present.

