Capillarity & Capillary Rise – definition & formula dervation

In this post, we have discussed capillarity and Capillary Rise. We also did the derivation of the formula of the height for Capillary Rise. We have added one assignment at the end of this post, that you must try (also check the solution – the link is provided)

---

Capillarity

If a capillary tube of glass is dipped in liquid like water, the liquid rises in the tube, but when the capillary tube is dipped in a liquid, like mercury, the level of liquid falls in the tube.

This phenomenon of the rise or fall of a liquid in the capillary is called capillarity.

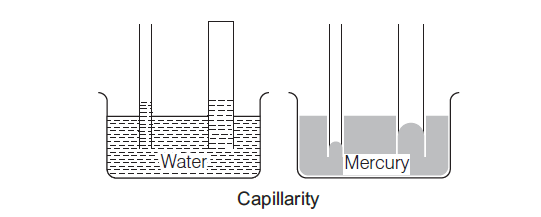
Some examples of capillarity are given below

(i) We use towels for drying our skin.
(ii) In trees sap rises due to vessels. It is similar to capillary action.

Capillary Rise | derivation of the formula of the height for Capillary Rise

One application of the pressure difference across a curved surface is the water rises up in a narrow tube (capillary) in spite of gravity. Consider a capillary of radius R is inserted into a vessel containing water.

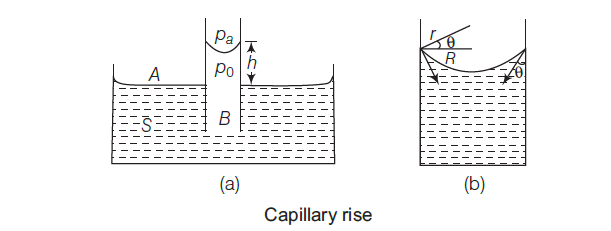
The surface of the water in the capillary becomes concave. It means that there must be a pressure difference between the two sides of the meniscus. (figure 2)

So, (p_a – p_o )= (2 S/ r)
= 2S/(R sec θ)
= (2S/R) cos θ …(i)
where r = radius of curvature of the concave meniscus.

and, θ = angle of contact

Now, consider two points A and B (figure 2).

According to Pascal’s law, they must be at the same pressure, hence, P_A = P_B

=> P_a = P₀ + hρg (here, p_a = atmospheric pressure)

=> P_a – P₀ = hρg … (ii)

From Eqs. (i) and (ii), we get
hρg = (2S/R) cos θ

Hence, the height of the rise of liquid in the capillary is given by

h = (2S cos θ)/ (Rρg)

Assignment

A glass tube of radius 0.4 mm is dipped vertically in the water. Find up to what height, the water will rise in the capillary. If the tube is inclined at an angle of 60° with the vertical, how much length of the capillary is occupied by water?
(Take, the surface tension of water = 7.0 × 10⁻² Nm⁻¹ and density of water = 10³ kg m ⁻³ )

check the Solution