Work done by a force
Last updated on May 16th, 2022 at 08:47 pm
Work done by a force – In Physics Work is done by a force only if the object on which the force is applied makes a displacement.
Without this displacement, work done is zero irrespective of the force applied.
Work done by a force depends on the 3 parameters:
(a) the force applied
(b) The displacement and
(c) The angle between the line of force applied and the displacement.
That’s why when you apply a force by pushing a wall and it never moves, you have not done any work in terms of physics. We will discuss versions of equations of work done by a force. We’ll study a few cases of work done by a force as well.
We will present this equation or formula in 2 formats. (a) simple (b) Vector
Equation of Work Done by a Force – A simple version of the Work Formula
The simple version of the equation of work is as follows: (considering that the displacement happens in the direction of the applied force i.e. the angle between the line of force and the displacement of the body is 0 degree)
Work = product of the magnitude of Force & magnitude of Displacement ( when the angle between the line of force and the displacement of the body is 0 degrees)
i.e. W=F S, Here W=Work done, F=applied force on the object, and S=the displacement of the object. Here, the direction of F is same as that of S.
Equation of Work Done by a Force – Vector Representation of Work formula
If we consider the Vector representation of the Work, Then we can write it as the dot product of Force and Displacement.
So we can write Work = Force . Displacement
or, W = F . S = FS Cos θ, where θ is the angle between the line of force and the displacement.
When θ = 0 degrees, i.e. the Force and the displacement are pointing towards the same direction, W = FS, as we have shown in the previous section.
The Meaning of θ: As said above, the angle θ is the angle between the force vector and the displacement vector. In all the following situations, θ = 0 degrees.
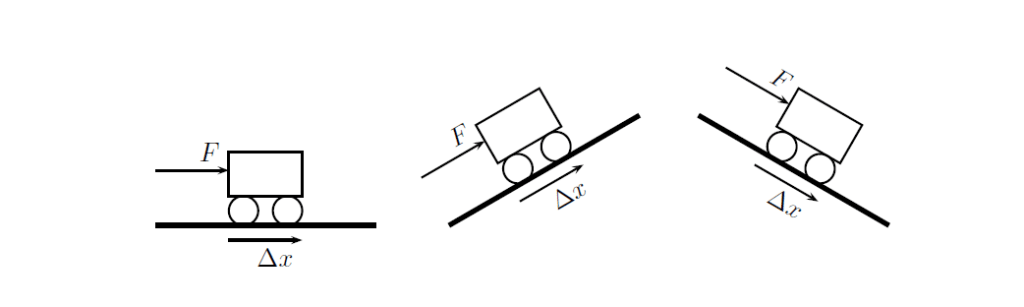
When θ = 180 degrees, i.e. the Force and the displacement are pointing to opposite directions, then W = F S cos 180 degree = F S (-1) = – F S. Here the – sign denotes that the displacement happens just in the opposite direction of the applied force.
Positive Work and Negative Work – differences
The work done by an object can be positive or negative. Since force (F) and displacement (s) are both vectors, the result of the Work equation (W = F . S = FS Cos θ) depends on their directions:
• If F acts in the same direction as the motion then positive work is being done. In this case, the object on which the force is applied gains energy.
• If the direction of motion and F are opposite, then negative work is being done. This means that energy is transferred in the opposite direction. For example, if you try to push a car uphill by applying a force up the slope but the car rolls down the hill you are doing negative work on the car. Alternatively, the car is doing positive work on you!
CASE STUDIES – work done
Case 1: A person lifts an object from the ground to his head top – work done by gravity

Here Force being applied on the object is the gravity or the weight of the object, against which work needs to be done by the person to lift it from the ground.
So Force (F) applied by the gravity = Mg where M = mass of the object,
g = acceleration due to gravity and together Mg is the weight of the object.
Note that this weight is pointing towards the center of the earth and the object needs to be lifted in the opposite direction of the force of gravity.
Displacement = height of the person = H.
The direction of the displacement = upwards i.e., opposite to the direction of the gravity
So, the angle between the line of force and the displacement is 180 degrees.
So Work done (W) by the gravity = Mg H cos 180 degree
= Mg H (-1) = – Mg H.
Case 2: A person drops an object from his head top to the ground – What is the Work done by gravity?
In this case, Force applied to the object is the same as the above case i.e Mg.
The displacement is the same as the first case (H). but in this case, displacement is happening in the direction of the force, so the angle between force and displacement is zero degrees.
So we get the Work done as Mg H cos 0 degrees =Mg H (1)= MgH
Case 3: Summation of case 1 and 2 – Work done
In this case, a person lifts an object first from the ground and then drops it to the ground again. Here we can get the work done (by the gravity) of this entire loop in 2 ways:
1) Way 1: As finally displacement(S) of the object is zero, so work done is zero.
2) Way 2: This case is the summation of case 1 and Case 2.
So if we consider the total work done by gravity = work done by gravity while the load is lifted + work done by gravity while the object dropped = – MgH + MgH = 0
Case 4: What is the work done If we push a wall and it doesn’t move
Case 4: We are pushing a wall but it doesn’t move
– We apply force (action) on the wall.
– The wall applies an equal and opposite force on us (reaction)
– If we don’t see it moving, so the displacement of the wall along the line of force is zero.
– We know that in this case, W = FS
– Here force is non-zero, but displacement along the line of force=0. Hence work done is zero.

