How does the speed of sound in air change with a change in temperature?
The speed of sound in the air changes when the temperature changes. In this article, we will study more with the help of a graph and also come up with an equation relevant to this variation.
Graph showing Speed of sound in air versus temperature
For temperatures near 0°C, the relationship between the speed of sound in the air with the temperature is approximately linear. Figure 1 shows a graph of the speed of sound in air as a function of temperature.
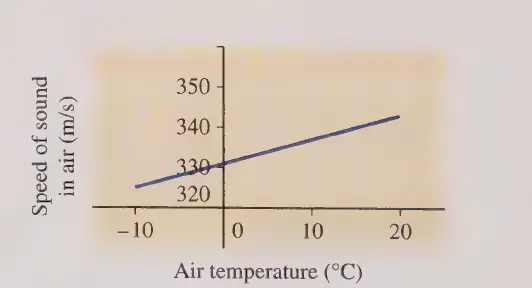
plotted as a function of temperature, valid for
temperatures near 0°C.
Notice that at 0°C the speed of sound in air is 331 m/s, and the speed increases by about 6 m/s for every 10°C rise in temperature.
In the limited temperature range we consider here, the increase, to three significant digits, is 0.606 (m/s)/°C.
Equation showing how the Speed of sound in air varies with temperature
Thus, the equation of the line on the graph yields the speed of sound in air:
v = 331 m/s + 0.606 (m/s)/°C X T
=> v = [331 + 0.606 T] m/s
where T is the temperature of the air in degrees Celsius (°C).
Also, know more about the Speed of sound in different mediums.
Numerical Problem (using the speed of sound and temperature equation)
The fog horn of a fishing trawler is sounded, and the sound reflects off a cliff and is received 6.4 seconds later back at the trawler. If the air temperature is -8.0°C, how far is the trawler from the cliff?
Solution:
Temperature T = -8.0°C
First, we find the speed of the sound in the air.
v = [331 + 0.606 T] m/s
=> v = 331 + 0.606x(-8) m/s
=>v = 331 – 4.8 = 326 m/s
The time taken by the sound for to and fro travel = 6.4 s
Hence, the time taken by the sound to travel from source to cliff = 6.4/2 = 3.2 s
Now, d = vt where t = 3.2 s
= 326 m/s X 3.2 s
= 1.0 X 103 m (to two significant digits)
Thus, the trawler is 1.0 km from the cliff.
Related: Speed of sound in different mediums.
