Derive the relation between Linear displacement and Angular displacement

Last updated on February 8th, 2024 at 10:26 am

We will derive the Relationship between linear displacement and angular displacement.

Relationship formula (to be derived)

The relationship is actually this: Linear Displacement = Angular Displacement x Radius of the Circular path

Derivation [step-by-step]

Say a point object is moving in a circular path of radius r. Let’s say the center of this circular path is O.

At some point in time say the particle is at point P on the circumference of the circle. At this moment the radial vector of this motion is OP.

After a time gap of t, the position of the object becomes Q (obviously on the circumference of the same circle) and the radial vector is OQ.

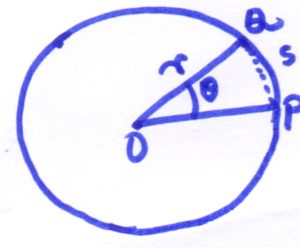
Now say the angle between OP and OQ is θ (theta). Hence the angular displacement of the particle in time duration t is θ.

In addition to this angular displacement, the particle is having a linear displacement as well when traveling from point P to Q.

Here PQ is the linear displacement, and say it is designated as s.

Now consider the right-angled triangle ΔOPQ.
Here using the Trigonometry we get, Sine θ = PQ /OQ = s/r ________________ (1)  
[ When P and Q are very close then PQ can be considered as a straight line = s.
Note: OQ is the radius r of the circle ]

Now, as per Trigonometry, if the angle θ is very small then Sine θ is equal to θ.

So from equation (1), we get
θ = s/r  i.e., s= θ r ______________(2).

Here we get the relation between linear displacement and angular displacement.

Linear Displacement = Angular Displacement x Radius of the Circular path

Reference post: linear and circular motion – 3 selected quantities & relationships