omega symbol in physics | omega symbol meaning in physics (ω)

Last updated on May 21st, 2023 at 09:29 pm

Omega symbol (ω) in physics denotes angular velocity or angular speed in a circular motion.

In this post, we will discuss ω (omega) which is the symbol used to denote the angular speed or angular velocity in a circular motion.

In linear or straight-line motion, we measure speed by looking at how much distance is covered each second. We can do that in circular motion too, but it’s often better to use angular speed, ω, in terms of angular displacement and time duration.

When an object is moving continuously and uniformly in circles, the angular velocity and the linear speed of the object around the circumference will both be constant, and they are closely related.

For continuous uniform circular motion, ω=2π/T = 2πf.

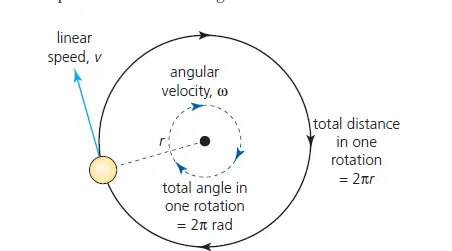
The linear speed of an object moving uniformly in a circle, v = 2πr/T.

Therefore, angular velocity, ω, and linear speed, v, are related by the simple equation v=ωr

Now, we will first define omega (ω), and then list down a few important equations of ω.
After this, we will derive the relationship between linear speed and angular speed ω.

Omega or ω

Angular speed omega(ω) measures the angle (measured in radians) covered by a body in circular motion per second.

In other words, Angular velocity (ω) is the angular displacement made per unit time.

Unit of omega (ω) is radian/second.

Equations of omega (ω) or angular speed

ω =angular displacement/time = Δθ/Δt, Where: Δθ = angle in radians, and Δt = time taken in seconds……………………………(1)

If you consider that the time taken for a complete rotation is the time period, T, then we can write another expression or equation for Angular speed omega (ω).

ω =2π/T ………………………………………(2)
[because 2π is the angle covered (in radians) when a complete circle is traveled]

The 3rd equation of omega is in terms of the frequency of the circular motion.

As we know, Time period = 1/frequency, hence T = 1/f
=> ω =2π/T
=> ω =2πf ………………………………………(3)

Relationship between Linear speed and angular speed (ω)

Say, a body is going around in a circle of radius, r, and traveling at a linear speed of v m/s:
The distance covered by the body in 1 rotation = 2πr
The time for one rotation = T, the time period.

Linear speed v = 2πr/T
=> v = 2πrf [as frequency f = 1/Time period]
=>v/r = 2πf
As per equation (3) above, v/r = ω
=>v = ωr [This is the relationship between Linear speed (v) and angular speed (ω)