Conservative force work done around a closed loop is zero – prove that

Work done by a conservative force in a closed loop is zero. We will show that mathematically here.

Read this related topic: Conservative force vs Non-conservative force – a comparative study

Work done by a Conservative force in moving a particle around a closed loop is zero – how to prove it

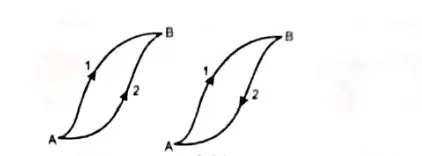
As per the definition, we know that a force is conservative if the work done by the force in displacing a particle from one point to another is independent of the path followed by the particle and depends only on the endpoints.

Suppose a particle moves from point A to point B along either path 1 or path 2, as shown in Figure 1(a). If a conservative force F acts on the particle, then the work done on the particle is the same along the two paths.

Mathematically, we can write

W_AB (along path1) = W_AB (along path 2) …..(i)

Now suppose the particle moves in a round trip, from point A to point B along path 1 and then back to point A along path 2, as shown in figure 1 (b).

For a conservative force,

Work done on the particle along path 2 from A to B = –  Work done on the particle along path 2 from B to A

i.e.,

W_AB(along path 2) = – W_BA(along path2)…(ii)

From (i) and (ii), we have

W_AB(along path 1) = -W_BA (along path2)

or

W_AB(along path 1) + W_BA(along path2) = 0

or W_closed path = 0

Hence a force is conservative if the work done by the force in moving a particle around any closed path is zero.