Torque on a current loop in a uniform magnetic field class 12
Last updated on April 17th, 2023 at 05:35 pm
In this post, we will know about the Torque on a current loop in a uniform magnetic field. We will also derive its equation. If a loop of current-carrying wire is placed in a uniform magnetic field (B) then it experiences no net force but a torque acts on it. This torque tends to rotate the loop to bring its plane perpendicular to the field direction. In other words, the torque tends to rotate the loop in such a way that the normal line drawn on the plane of the loop becomes parallel to the magnetic field direction. This is the principle that underlines the operation of all electric motors, meters, etc.
- Torque on a current loop in a uniform magnetic field
- Net force on a current-carrying loop in a uniform magnetic field is zero
- How torque is exerted on a current-carrying loop in a uniform magnetic field
- Formula of torque on a current loop in a uniform magnetic field | derivation of the equation of the torque
- When is the torque on a current loop in the magnetic field maximum?
- When is the torque on a current loop in the magnetic field minimum?
Torque on a current loop in a uniform magnetic field
Here, we will see how torque is generated and how to get its equation.
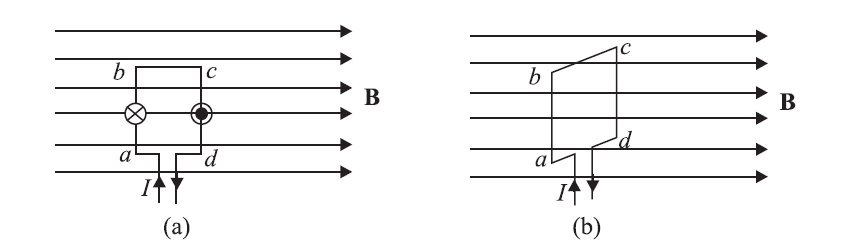
and (b) the loop is perpendicular to the field.
Net force on a current-carrying loop in a uniform magnetic field is zero
Let us examine the force on each side of a rectangular current-carrying loop where the plane is parallel to a uniform magnetic field B.
When the loop is parallel to the field
The sides ad and bc of the loop are parallel to B. So no force will act on them.
When the loop is perpendicular to the field
Sides ab and cd are, however, perpendicular to B, and these experience maximum force. We can easily find the direction of the force on ab and cd. In fact, |Fab|=|Fcd|, and these act in opposite directions. Therefore, there is no net force on the loop.
So, it’s evident that irrespective of the loop’s position with respect to the direction of the magnetic field, the net force on the loop is zero.
How torque is exerted on a current-carrying loop in a uniform magnetic field
Since Fab and Fcd do not act along the same line, they exert a torque on the loop that tends to turn it. This holds good for a current loop of any shape in a magnetic field. This means just like the rectangular loop shown in the figure above, a current-carrying circular loop in a uniform magnetic field will also face a torque on it.
In case the plane of the loop is perpendicular to the magnetic field, there would neither be a net force nor a net torque on it. This will be clear if we study the formula of the torque we will deal with now.
Formula of torque on a current loop in a uniform magnetic field | derivation of the equation of the torque
Referring to figure 1[a]: say the length of side bc=ad = p = perpendicular distance between two opposite forces causing the torque in figure 1a.
and, let’s say the length of ab = cd = q = length of current (I) carrying sides causing torque in Figure 1a.
Now, again referring to figure 1[a]: Torque τ = F p = BIq p = BI pq = BIA
Here, A is the area of the loop.
If there are N number of loops, then τ =NBIA = NIA B
NIA is called magnetic moment [m]. [Read more about Magnetic Moment]
τ = NIA B = m B
If there is an angle θ between B and normal to the plane of the loop then
τ = m B sin θ
=> τ = m x B
=> τ = NIAB sin θ
When is the torque on a current loop in the magnetic field maximum?
Torque τ = NIAB sin θ
When θ = 90o then torque becomes maximum. That means when the angle between B and normal to the plane of the loop is 90o then the torque is maximum. This also means when the plane of the loop is parallel to B then the torque becomes maximum.
When is the torque on a current loop in the magnetic field minimum?
τ = NIAB sin θ
Hence, when θ = 0o then torque becomes minimum. That means when the angle between B and normal to the plane of the loop is 0o then the torque is minimum. This also means when the plane of the loop is perpendicular to B then the torque becomes minimum.

