Magnetic field due to infinitely long straight conductor carrying current
In this post, we will apply the Biot-Savart law to derive an equation for the Magnetic field due to an infinitely long straight conductor carrying current.
Magnetic field due to an infinitely long straight conductor carrying current – derivation
XY is an infinitely long straight conductor carrying a current I (Figure below). P is a point at a distance a from the conductor. AB is a small element of length dl. θ is the angle between the current element I dl and the line joining the element dl and the point P.
According to Biot- Savart law, the magnetic field at the point P in a vacuum due to the current element Idl is
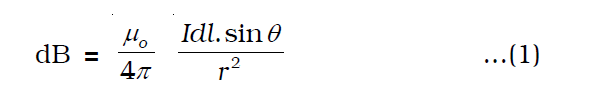
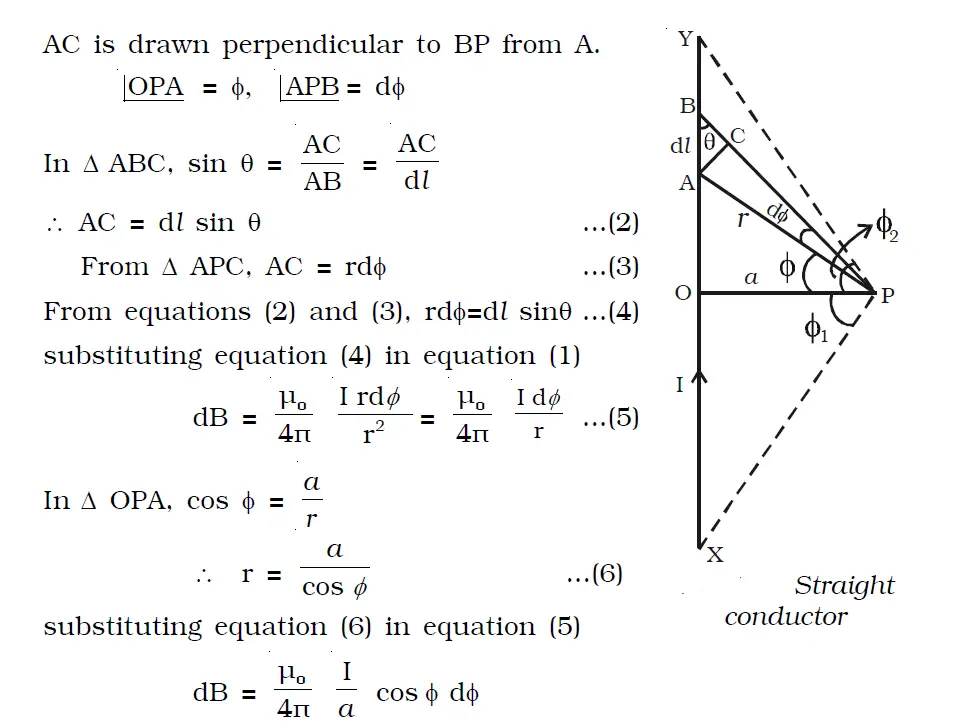

Thus, we can derive an equation for the Magnetic field due to an infinitely long straight conductor carrying current.
formulas of the Magnetic field due to a long straight current-carrying conductor
For a finitely long conductor in a vacuum, at a point at a distance a from the conductor, the magnetic field B = [(μ0 I)/(4πa)](sin Φ1 + sin Φ2)
For an infinitely long conductor in a vacuum, at a point at a distance a from the conductor, the magnetic field B = (μ0 I)/(2πa)
If the infinitely long conductor is placed in a medium of permeability μ, then at a point at a distance a from the conductor, the magnetic field B = (μ I)/(2πa)
