Biot-Savart Law statement, formula, derivation

Last updated on August 23rd, 2023 at 09:16 am

In this post, we will cover the Biot-Savart Law statement, formula, and derivation.

Biot and Savart conducted many experiments to determine the factors on which the magnetic field due to the current in a conductor depends. The results of the experiments are summarized by the Biot-Savart law.

Biot-Savart law

Let us consider a conductor XY carrying a current I (Fig 1).

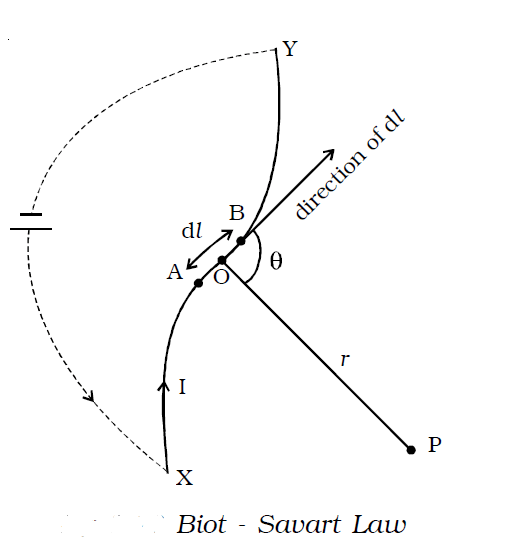
AB = dl is a small element of the conductor. P is a point at a distance r from the midpoint O of AB.

Biot-Savart Law statement

According to Biot and Savart, the magnetic induction dB at P due to the element of length dl is

(i) directly proportional to the current (I)
(ii) directly proportional to the length of the element (dl )
(iii) directly proportional to the sine of the angle between dl and the line joining element dl and the point P (sin θ)
(iv) inversely proportional to the square of the distance of the point from the element (1/r²)

Biot-Savart Law formula & derivation

∴ dB α (I dl sin θ) /r²
=> dB = K (I dl sin θ) /r²
Here, K is the constant of proportionality

The constant K =μ/4π, where μ is the permeability of the medium.

dB = (μ/4π) (I dl sin θ) /r²

dB = (μ Idl sin θ) /(4πr²)

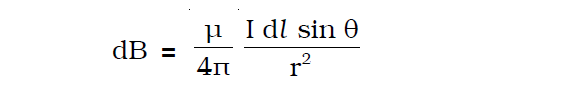
μ = μ_r μ₀ where μ_r is the relative permeability of the medium and μ₀ is the permeability of free space. μ₀ = 4π × 10^–7 henry/metre.

In air,
dB = (μ₀ Idl sin θ) /(4πr²)

scalar and vector forms of Biot-Savart law

Here are the scalar and vector forms of the Biot-Savart law.

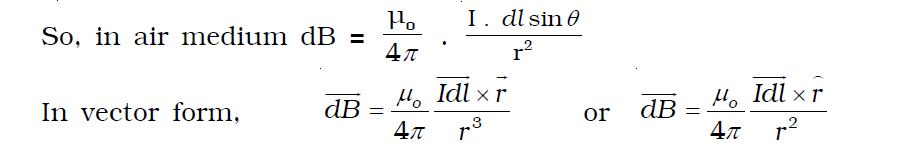
The direction of dB is perpendicular to the plane containing the current element Idl and r (i.e. plane of the paper) and acts inwards. The unit of magnetic induction is tesla (or) Weber m^-2.

[ Also read Ampere’s Circuital Law – formula, derivation]