Numerical problems based on the motion of a charge in a uniform electric field between two parallel plates

Last updated on March 16th, 2022 at 02:30 pm

In this post, let’s solve Numerical problems based on the motion of a charge in a uniform electric field between two parallel plates.

In the case of the motion of a charge in a uniform electric field between two parallel plates, the acceleration is constant because of the constant force, so either the work-energy theorem or the laws of dynamics can be used. (Because the electric field is constant (uniform), the force acting on a charge q is also constant because F = qE.)

Numerical problem set

1 ) An electron enters the electric field between two charged parallel plates, as shown in Figure 1.

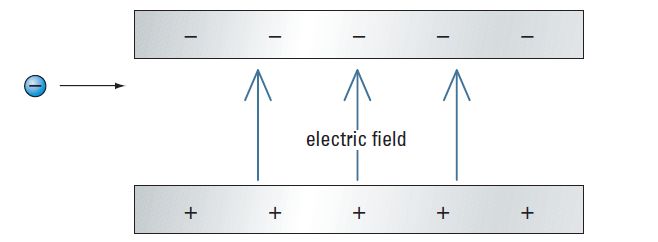
(a) sketch the motion of the electron between the plates.
(b) If the electron experiences a downward acceleration of 2.00 x 10¹⁷ m/s² due to the electric field between the plates, determine the time taken for the electron to travel 0.0100 m to the positive plate.

Solution:

Given
a = 2.00 x 10¹⁷ m/s² (down)

d = 0.0100 m

Required to find out
(a) sketch of the electron’s motion
(b) time t

Analysis and Solution
(a) The electron’s acceleration is downward, so the motion of the electron will follow a parabolic path to the positive plate (Figure 2), similar to the projectile motion of an object traveling horizontally to the surface of Earth and experiencing downward acceleration due to gravity.

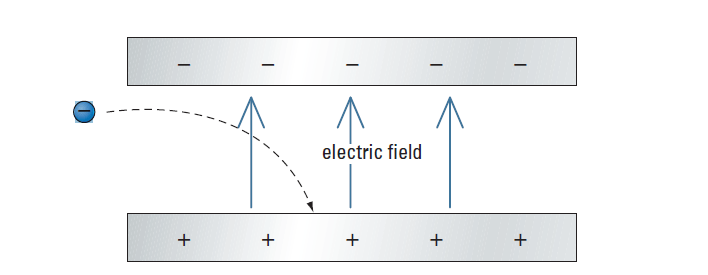
b) We will use this equation: d = ut + (1/2)at²

here, u = 0

d = (1/2)at² ….(i)

Here, the time required for the electron to fall to the positive plate = t

t = (2d/a)^1/2 = (2×0.0100/2.00 x 10¹⁷ )^1/2 sec = 3.16 x 10^-10 secs.