how acceleration due to gravity varies with latitudes

Last updated on April 23rd, 2022 at 02:21 pm

In this post, we will see how acceleration due to gravity varies with latitudes.

acceleration due to gravity(g) varies with latitudes – how?

Consider a point A on the earth’s surface where the line joining center O to A makes an angle θ with the equatorial plane as shown. The angle θ is said to be the latitude of point A´. (figure 1)

Let us place a small particle of mass m at A. Analysing the forces of on m, from the reference frame of the earth, we find two forces gravitational force (mg) and pseudo force (mω²r).

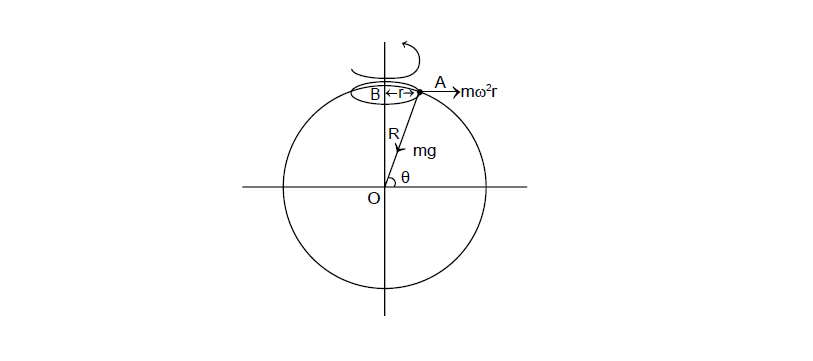
Here, r is the radius of the circular path followed by m.

r = R cos θ

The resultant force of masses m is given by
F = [m²g² + m²ω⁴r² + 2(mg)(mω²r) cos(π − θ)]^1/2

The effective gravity at point A,

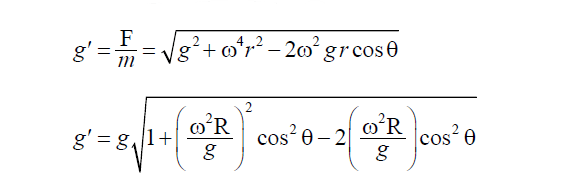
…………………………………………………….. (1)
where g is the acceleration due to gravity at the surface of the earth neglecting the effect of the rotation.

(a) acceleration due to gravity at poles (due to the latitudes of poles)
θ = 90º
So, from equation (1)
⇒ g’ = g
Hence, the rotation of the earth has no effect on the gravity at the poles.

(b) acceleration due to gravity at equator (due to the latitude of equator)
θ = 0º
So, from equation (1)
=> g’ = g [ 1 – (ω²R/g)]