Factors affecting the capacitance of a parallel-plate capacitor – detailed revision notes
Last updated on April 18th, 2022 at 05:55 pm
In this post, we will discuss different factors that affect the capacitance of a parallel-plate capacitor.
The greater the capacitance of a capacitor the greater the charge held by it for the same applied voltage.
The factors affecting the capacitance of a parallel-plate capacitor are:
- Plate area
- Plate spacing (distance between the plates)
- Dielectric material
How plate area of a capacitor affects the capacitance of a capacitor?
If the plate area of a capacitor is increased there is a corresponding increase in capacitance, provided there is no change in the distance between the plates or in the dielectric material.
Capacitance is directly proportional to plate area. Figure 1 and Figure 2 demonstrate this.
C α A, where A is the area of the plates in m2
When two capacitors are placed in parallel, the plate area is increased and so the capacitance is increased.
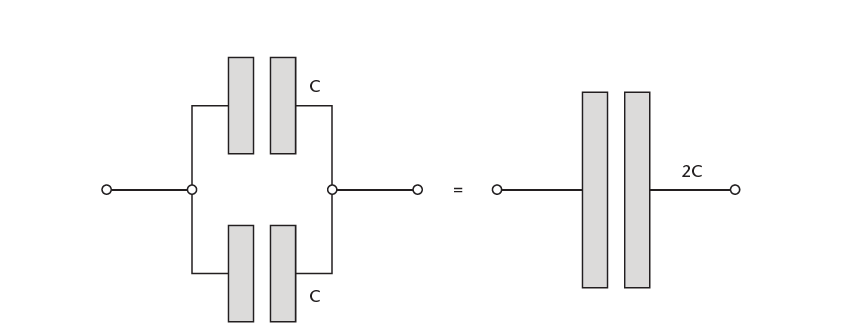
When 2 capacitors with equal capacitance (C for each) are connected in parallel, then the net capacitance Cparallel is found like this:
Cparallel = C + C = 2C. This shows that When two capacitors are placed in parallel, the plate area is increased and so the capacitance is increased as well.
In the case of Capacitors of different values: For example, Two capacitors of the value 10 μF and 6 μF are connected in parallel. Find out the net or equivalent capacitance.
Solution
CT = C1 + C2
CT =10μF + 6μF = 16μF
This result shows that When two capacitors are placed in parallel, the plate area is increased and so the capacitance is increased.
How plate spacing of a capacitor affects the capacitance of a capacitor?
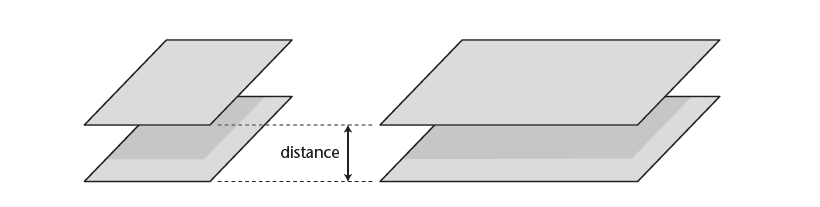
The capacitance of a capacitor changes when the distance between the plates changes. It increases when the plates are brought closer together and decreases when they have moved further apart.
Refer to Figure 3. Plates A have more capacitance than plates B.
Capacitance is inversely proportional to the distance between the plates;
C α 1/d, where d = distance between plates in m.
How Dielectric Material affects the capacitance of a capacitor?
Using the same plates fixed a certain distance apart, the capacitance will change if different insulating materials are used for the dielectric. The effect of different materials is compared to that of air – that is, if the capacitor has a given capacitance when air is used as the dielectric, other materials used instead of air will multiply the capacitance by a certain amount called the ‘dielectric
constant’.
Changing the Dielectric Material changes the capacitance as demonstrated in Figure 4.
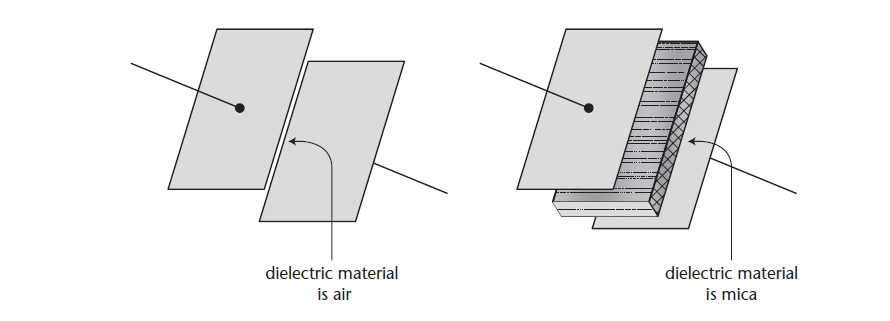
For example, some types of oiled paper have a dielectric constant of 3; and if such oiled or the waxed paper is placed between the plates, the capacitance will be three times greater than it would be if the dielectric was air.
Different materials have different dielectric constants and so will alter the capacitance when they are placed between the plates to act as the dielectric. Listed below are the Dielectric Constants for typical materials.
[ Read: Capacitance formulas for Parallel-plate capacitors ]
Why does the capacitance of a capacitor change with a dielectric material between the plates?
When a dielectric is inserted between the plates of the capacitor it is polarized, the extreme surface of the dielectric near the negative plate becomes positively charged and the extreme surface of the dielectric near the positive plate becomes negatively charged.
Then an electric field arises that opposes the electric field of the capacitor making it weak, and the potential difference also decreases according to (V= Ed).
As a result, the capacitance increases because C is inversely proportional to the potential difference (V) (Figure 5)
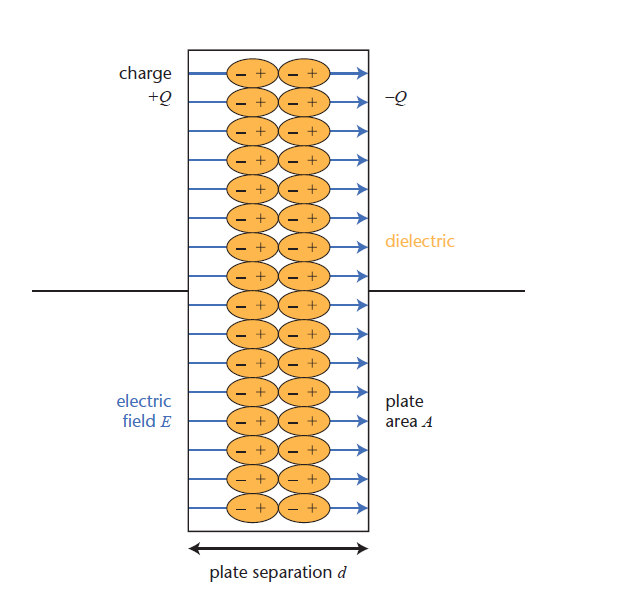
How does the capacitance of a capacitor change with the type of dielectric material between the plates?
As the value of the dielectric constant (K) increases, the capacitance of the parallel-plate capacitor also increases.
Because a higher value of K means higher polarization of the dielectric and a higher value of the opposing electric field.
As a result, the electric field of the capacitor gets weaker. This, in turn, makes the potential difference lesser. This causes finally a bigger capacitance of the parallel-plate capacitors.
