Equivalent capacitance for Capacitors – derivation
Last updated on May 18th, 2022 at 01:14 pm
Capacitors are manufactured with certain standard capacitances and working voltages. However, these standard values may not be the ones we actually need in a particular application. We can obtain the values we need by combining capacitors.
Many combinations of capacitors are possible, but the simplest combinations are a series connection and a parallel connection.
Capacitors in series connection
Capacitors in Series Figure 1a is a schematic diagram of a series connection. Two capacitors are connected in series (one after the other) by conducting wires between points a and b.
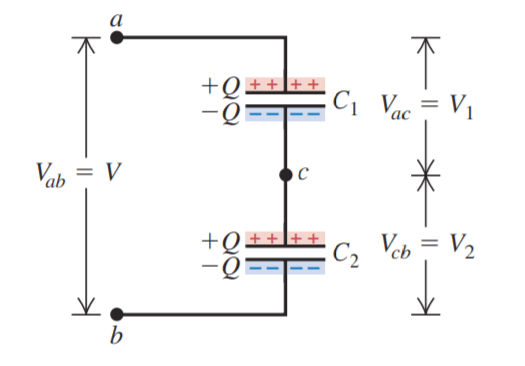
figure 1(a) Two capacitors in series
Both capacitors are initially uncharged. When a constant positive potential difference Vab is applied between points a and b, the capacitors become charged; the figure shows that the charge on all conducting plates has the same magnitude.
Also, note that: Vac + Vcb = Vab. [ sum of voltages across capacitors in series equals the potential difference applied]
Why does the charge on all conducting plates of capacitors in series connection has the same magnitude?
Referring to figure 1a, note first that the top plate of C1 acquires a positive charge Q. The electric field of this positive charge pulls the negative charge up to the bottom plate of C1 until all of the field lines that begin on the top plate end on the bottom plate. This requires that the bottom plate have charge -Q.
These negative charges had to come from the top plate of C2, which becomes positively charged with charge +Q. This positive charge then pulls negative charge -Q from the connection at point b onto the bottom plate of C2.
The total charge on the lower plate of C1 and the upper plate of C2 together must always be zero because these plates aren’t connected to anything except each other. Thus in a series connection, the magnitude of the charge on all plates is the same.
Equivalent capacitance for Capacitors in series – derivation

figure 1(a) Two capacitors in series
Let’s refer to figure 1a where capacitors are in series. We will derive the formula for the equivalent capacitance for Capacitors in series using this diagram.
We can write the potential differences between points a and c, c and b, and a and b as:
Vac = V1 = Q/C1
Vcb = V2 = Q/C2
Vab = V = V1 + V2 = Q/C1 + Q/C2 = Q (1/C1 + 1/C2)
Hence, V/Q = (1/C1 + 1/C2) ……….. (1)
Let, the equivalent capacitance of the series combination is Ceq
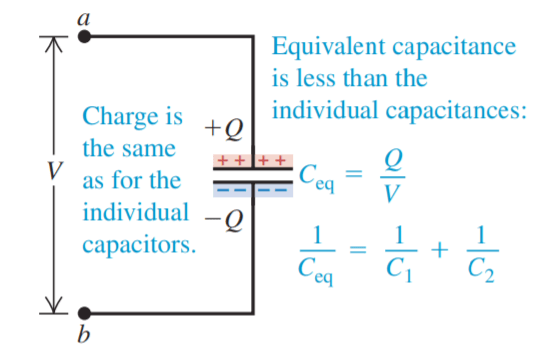
The equivalent capacitance Ceq of the series combination is defined as the capacitance of a single capacitor that can replace the combination capacitors C1 and C2 in series.
Hence from figure 1(b), Ceq = Q/V
or 1/Ceq = V/Q ………. (2)
Combining equation (1) and (2), 1/Ceq = 1/C1 + 1/C2
This is how we can derive the formula of the equivalent capacitance of capacitors connected in series.
We can extend this analysis to any number of capacitors in series. We find the following result for the reciprocal of the equivalent capacitance:
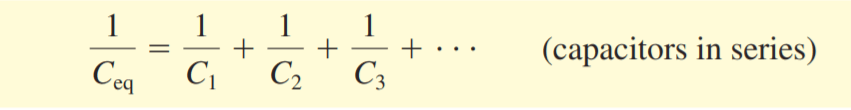
The reciprocal of the equivalent capacitance of a series combination equals the sum of the reciprocals of the individual capacitances. In a series connection, the equivalent capacitance is always less than any individual capacitance.
Capacitors in Parallel connection
The arrangement shown in Fig. 2a is called a parallel connection.
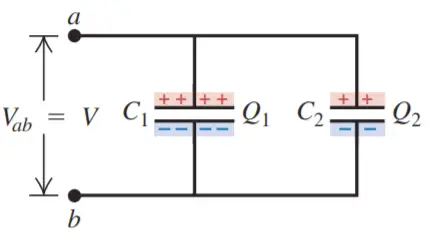
The capacitors in parallel have the same potential V.
The charge on each capacitor depends on its capacitance:
Q1 = C1 V
Q2 = C2 V
Two capacitors are connected in parallel between points a and b. In this case, the upper plates of the two capacitors are connected by conducting wires to form an equipotential surface, and the lower plates form another. Hence in a parallel connection, the potential difference for all individual capacitors is the same and is equal to Vab = V.
Now, let’s find out the equivalent capacitance Ceq of the capacitors connected in parallel.
Equivalent capacitance for Capacitors in Parallel – derivation
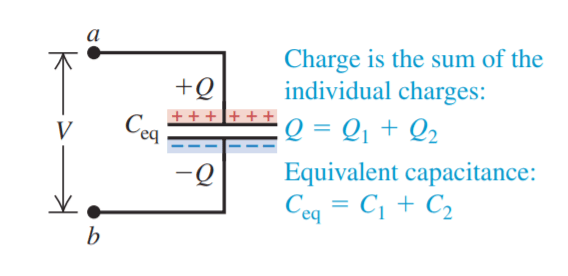
The charges Q1 and Q2 are not necessarily equal, however since charges can reach each capacitor independently from the source (such as a battery) of the voltage Vab.
The charges are Q1 = C1 V and Q2 = C2 V
The total charge Q of the combination, and thus the total charge on the equivalent capacitor, is
Q = Q1 + Q2 = (C1 + C2) V
so, Q/V = C1 + C2 ………… (3)
The parallel combination is equivalent to a single capacitor with the same total charge Q = Q1 + Q2 and potential difference V.
The equivalent capacitance of the combination, Ceq, is the same as the capacitance Q/V of this single equivalent capacitor.
Ceq = Q/V ……. (4)
So from 3 & 4 we can write for parallel combination of capacitors,
Ceq = C1 + C2
This is how we can derive the formula of the equivalent capacitance of capacitors connected in parallel.
In the same way, we can show that for any number of capacitors in parallel,
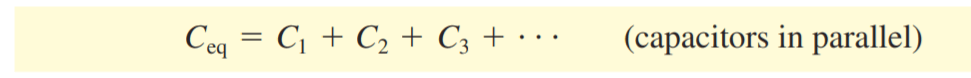
The equivalent capacitance of a parallel combination equals the sum of the individual capacitances. In a parallel connection, the equivalent capacitance is always greater than any individual capacitance.
