Implementation of Boolean function using multiplexer

Last updated on July 21st, 2023 at 08:52 am

In this post, with the title Implementation of Boolean function using Multiplexer, we will solve a numerical problem based on Multiplexers. We also see how to implement the Boolean function using Multiplexers. Here, we have used 8:1 MUX.

Implementation of Boolean function using Multiplexer

1 ) Problem: An 8-to-1 MUX has inputs A, B, and C connected to the selection inputs S₂, S₁, and S₀ respectively. The data inputs, D0 through D7, are as follows: D₁=D₂=D₇=0; D₃=D₅=1; D₀=D₄=D; D6=D’. Determine the Boolean expression that the MUX implements.

Solution: Any Boolean or logical expression can be easily implemented using a multiplexer.

If a Boolean expression has (n+1) variables, then the ‘n’ of these variables can be connected to the select lines of the multiplexer. The remaining single variable along with constants 1 and 0 is used as the input of the multiplexer.

For example, if D is the single variable, then the inputs of the multiplexer are D’, D, 1, and 0. By this method, any logical expression can be implemented.

Following this method, we can solve the above problem easily.

• The data inputs of the multiplexer, D0 through D7, are as follows: D1=D2=D7=0; D3=D5=1; D0=D4=D; D6=D’.
• The inputs A, B, and C are connected to the selection inputs S_2, S₁, and S₀ respectively.

Now considering the above two relations, we can draw the following truth table where input A is considered as MSB (most significant bit) and input D is the LSB (least significant bit) of the 4-variable function.

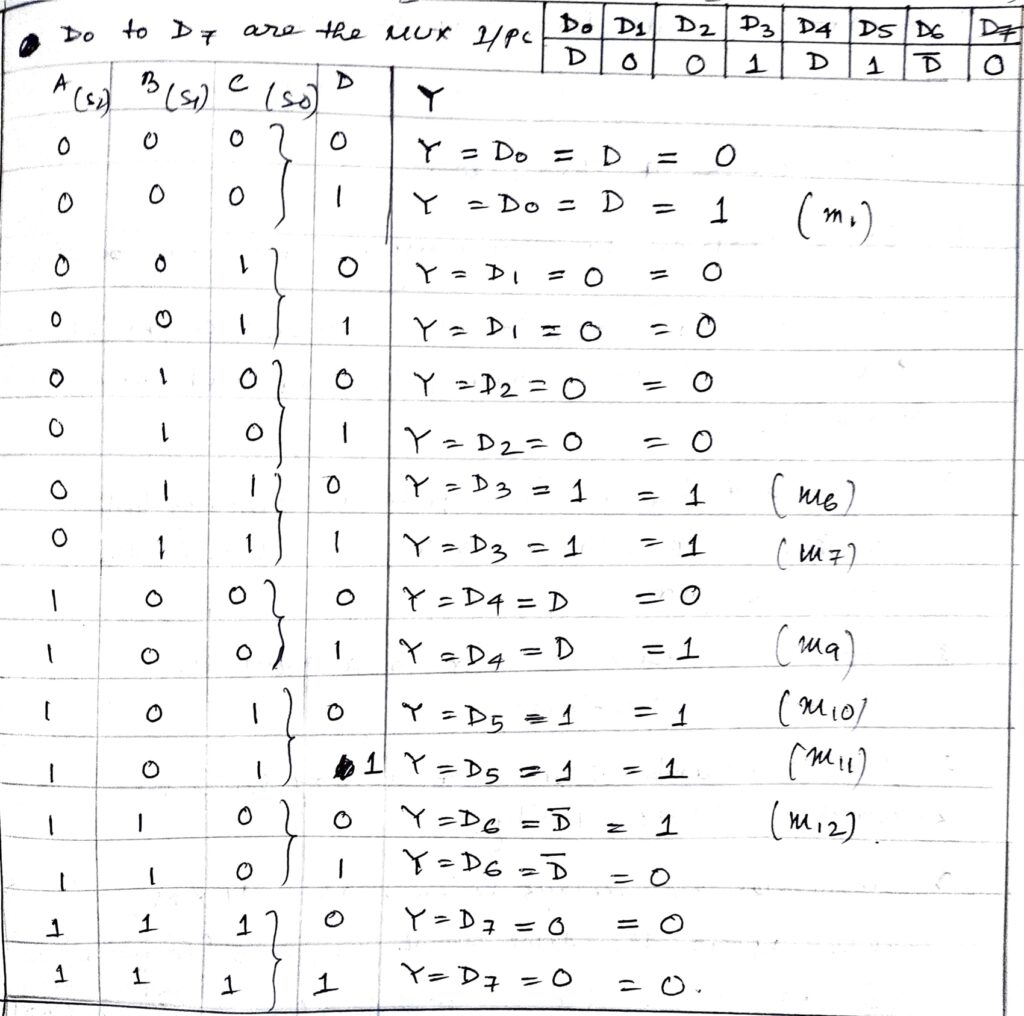
Now from the above truth table, it is clear that the function has 4 variables i.e. A, B, C, and D. And for the minterms, m₁, m₆, m₇, m₉, m₁₀, m₁₁, m_12, the output is logic 1.

So the Boolean function that the MUX implements is F(A, B, C, D)= ∑m(1,6,7,9,10,11,12).

Related reading you may refer to Full adder using Mux (using two 4:1 multiplexers)

Also, you may read, DeMorgan’s theorems of Boolean algebra