Snell’s law and its importance to calculate the refraction of light – with equation
Last updated on April 14th, 2021 at 05:21 pm
Snell’s Law comes into action in the case of refraction of light, which is the change in direction of a light ray as it goes from one medium to another.
As shown in Figure, a ray of light that encounters a change in medium is partially reflected, as if the boundary were a mirror. The part of the ray that goes through the second medium is bent, from an angle of incidence i in medium 1 to angle of refraction r in medium 2.
(Note that incident and refracted angles are measured with respect to the normal.)
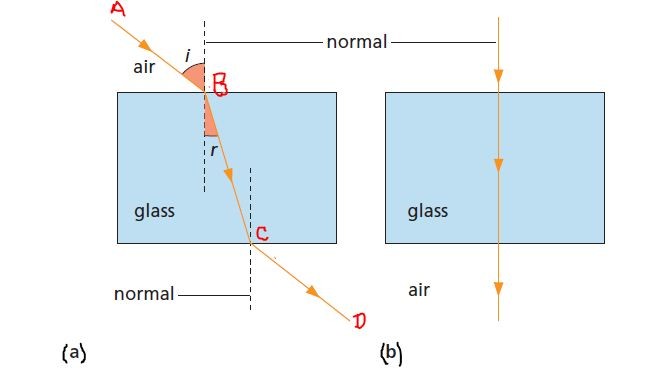
Snell’s Law and its equation or formula
As per Snell’s Law, for two give medium, the ratio of the sine of the angle of incidence and the sine of the angle of refraction is constant. It is expressed this way:
sin i / sin r = constant. …(i)
[where i = angle of incidence in medium 1 and r = angle of refraction in medium 2]
This constant is called the refractive index of medium 2 with respect to medium 1.
So Snell’s law can be further expressed as:
sin i / sin r = constant = 1µ2 = refractive index of medium 2 with respect to medium 1
Importance of Snell’s Law
If we know the index of refraction of different media or get those from the refractive index table, we can use Snell’s law to predict light’s path in those media. For example, a light ray coming from a fish underwater that strikes the water’s surface at an angle of 30° from the normal emerges in the air at about 42°. That’s why the fish appears to be at a much lesser depth than its actual depth.
