How to use Pascal’s principle (or Pascal’s law) in Hydraulic Car Lift?
Last updated on September 9th, 2021 at 02:06 pm
We will first see what Pascal’s Principle or Pascal’s Law states. Then we will find out with formula and diagram how to apply Pascal’s Law to explain the operating principle of Hydraulic Car Lift or hydraulic jack.
Pascal’s principle (or Pascal’s law)
Pascal’s Law states that Any change in the pressure applied to a completely enclosed fluid is transmitted undiminished to all parts of the fluid and the enclosing walls.
How to apply Pascal’s law to explain Hydraulic Car Lift operation
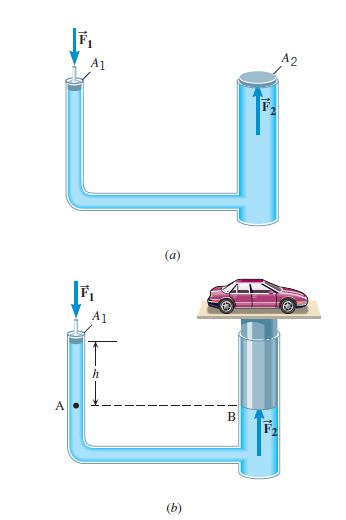
A hydraulic jack or hydraulic car lift has a platform on top of piston B (in figure 1 b) and is used in garages to lift cars.
Let’s discuss its operating principle or hydraulic principle using Pascal’s Law.
Figure (1)(a) shows two interconnected cylindrical chambers. The chambers have different diameters and, together with the connecting tube, are completely filled with a liquid. The larger chamber has a movable plunger at the top, while the smaller one is fitted with a movable piston.
On the left chamber piston, a vertically downward external force with magnitude F1 is exerted on an area A1.
So the downward pressure at a point immediately beneath the piston of the left chamber is P1 = F1/A1. ….. (1)
Now as per Pascal’s principle or Law the same pressure is transmitted undiminished to the plunger of the right chamber (larger one) top.
If we denote this upward pressure as P2 then we can say the following:
P1 =P2….. (2)
Now if the right chamber plumber has an area of A2 where the pressure is being transmitted, then the upward force being applied on the right chamber plunger is
F2 = P2 . A2
=> P2 = F2/A2. … (3)
So from all 3 equations above we get,
P1=P2
=> F1/A1 = F2/A2
=> F2 = (A2/A1). F1 ………… (4)
Now if A2 >> A1, that means a large upward force F2 can be transmitted to the right chamber plunger by applying a relatively much smaller downward force F1 at the left chamber piston.
Depending on the ratio of the areas A2 /A1, the force F2 can be large indeed, as in the familiar hydraulic car lift shown in Figure (1) (b).
Thus applying Pascal’s law a small force at one end of a completely enclosed fluid can transmit a greater force to the other end that can lift a heavy car. This summarizes the operating principle of the hydraulic car lift or hydraulic jack.

