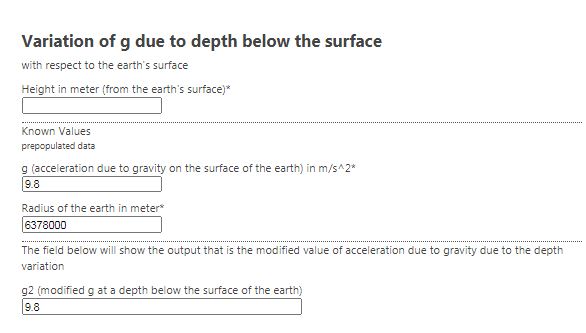
Formula for acceleration due to gravity at a depth h – with derivation

Last updated on April 19th, 2023 at 04:43 pm

In this post, we will discuss and derive the formula for the acceleration due to gravity at a depth h. As the depth from the earth’s surface is increased, the value of g falls. We will discuss and derive the equation that describes the change in the value of g due to depth from the earth’s surface.

Formula for the acceleration due to gravity at depth h

The formula for the acceleration due to gravity at depth h is expressed by the formula:
g2 = g (1 – h/R)
Here g2 is the acceleration due to gravity at depth h and R is the radius of the earth.
g denotes acceleration due to gravity on the earth’s surface.

For example, considering g = 9.8 m/s^2 on the earth’s surface, g2 at a depth of 1000 meter from the surface of the earth becomes 9.7984 m/s^2. [ check with online calculator ]

Derive the Formula for acceleration due to gravity at depth h | derivation of the formula of g at a depth

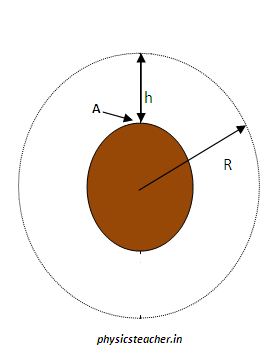
Let’s say, a body of mass m is resting at point A, where A is at a depth of h from the earth’s surface.

The distance of point A from the center of the earth = R – h,
where R is the radius of the earth.

Mass of inner sphere = (4/3). Π. (R-h)³. ρ

Here ρ is the density. and Π is 22/7.

Now at point A, the gravitational force on the object of mass m is

F = G M m/ (R-h)²

= G. [(4/3). Π. (R-h)³. ρ] m/(R-h)²

= G. (4/3). Π. (R-h). ρ. m

Again at point A, the acceleration due to gravity (say g2) = F/m = G. (4/3). Π. (R-h). ρ  _________________ (7)

Now we know at the earth’s surface, g = (4/3) Π R ρ G ( see the proof here: g formula on the surface of the earth using density)

Taking the ratio, again,

g2/g = [G. (4/3). Π. (R-h). ρ ] / [(4/3) Π R ρ G]

= (R-h) / R = 1 – h/R.

=> g2 = g (1 – h/R)

The formula for the acceleration due to gravity at depth h is represented with this equation:
=> g2 = g (1 – h/R)  ______ (8)
g2 is the acceleration due to gravity at a depth of h

You can use our online calculator to test the equation of g at a depth below the earth’s surface. Click the image below for the calculator page.