How to convert between degrees and radians -degree and radian conversion formulas
Last updated on January 25th, 2022 at 08:14 pm
Angular displacement is often expressed in one of three units. The first is the degree, and it is well known that there are 360 degrees in a circle.
The second unit is the revolution (rev), one revolution representing one complete turn of 360 degrees.
The most important unit from a scientific viewpoint, however, is the SI unit called the radian (rad). Here we will quickly find out how to convert between degrees and radians.
How to convert between degrees and radians? | degree and radian conversion
We will take the example of a CD (Compact Disc). Figure 1 shows how the radian is defined. A point P on the disc starts out on the stationary reference line, so that θ0 =0 rad, and the angular displacement is ∆θ = θ – θ0.
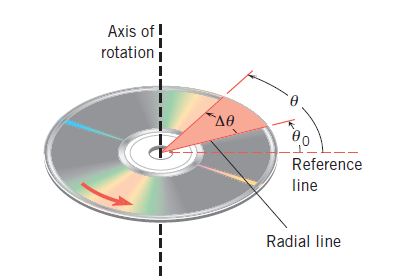
CD is the angle ∆θ
is defined to be the arc length s divided by
the radius r.
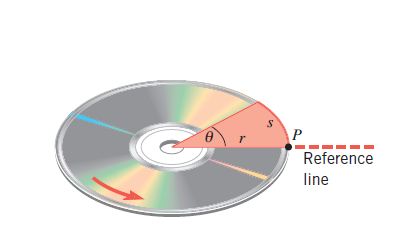
Now along with angular displacement, the CD makes linear displacement as well. As the disc rotates, the point traces out an arc of length s, which is measured along a circle of radius r. When θ is very minute, arc s is small straight line
Hence, Sin θ = s/r ….. (1)
As θ is minute, we can take Sin θ = θ.
So, modifying equation (1) we get, θ = s/r …………(2)
Equation (2.i) now defines the angle θ in radians:
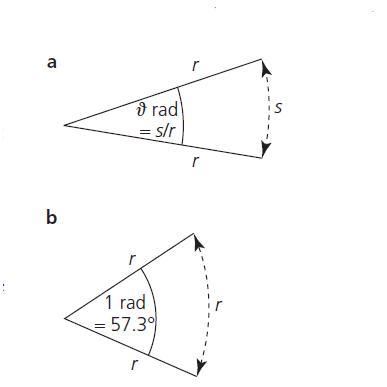
θ (in radians) = Arc Length / Radius = s/r …………….(2.i)
According to this definition, an angle in radians is the ratio of two lengths; for example,
meters/meters. In calculations, therefore, the radian is treated as a number without units.
To convert between degrees and radians, it is only necessary to remember that the arc
length s of an entire circle of radius r is the circumference 2πr.
Therefore, according to Equation 2, the number of radians that corresponds to 360 degrees, or one revolution, is θ = s/r=2πr/r = 2π rad
So, 360 degrees = 2π rad ……………………….. (3)
Again, 2π rad = 360 degrees
So, 1 rad = 360 degrees/2π = 57.3 degrees………………..(4)
So, we get two equations (3) and (4) to do the conversion between radian and degree.
Degrees and radians – summary
The use of degrees to measure angles is familiar to us in everyday life and in our early studies in mathematics and science, but it is not convenient mathematically because it is based on an arbitrary and historical choice of 360° for a complete revolution.
The ratio of the circumference of a circle, 2πr, to its radius, r, is a more logical basis for the measurement of angles. In this system 2πr/r (= 2π) becomes the measurement of one revolution, rather than 360°.
Although an angle like 2π is just a ratio, it is called 2π radians, commonly reduced to rad.
180° = π rad.
1 rad = 180°/π = 57.3°
In general, an angle in radians is equal to the distance along the arc of a circle divided by the radius, θ(rad) = s/r (figure 3)