Mechanical Advantage of a Lever with Formula

Last updated on May 18th, 2023 at 02:15 pm

The mechanical advantage of a lever is the ratio of the load the lever overcomes and the effort a person or system applies to the lever to overcome some load or resistance.
In simple words and as per the formula, it’s the ratio of load and effort.
The formula of the mechanical advantage(MA) of a lever is given as MA = load/effort.
Another form of this ma formula is MA = Effort Arm/Load Arm = EA/LA.

Example: Calculate the mechanical advantage if 500 N force is needed to overcome the load of 1000 N.
Solution: Effort = 500 N and Load = 1000 N
The formula of mechanical advantage is MA = Load/ Effort
Hence, MA  = 1000 / 500 => MA  = 2

Now, let’s find out more details about this MA of a lever.

What is the mechanical advantage of a lever?

The mechanical advantage of a lever is a number that indicates how a lever performs as a simple machine by transforming the input force or effort and this mechanical advantage of a lever is defined as the ratio of the load the lever overcomes and the effort a person or system applies to the lever to overcome some load or resistance. In simple words and as per the formula, it’s the ratio of load and effort.

Hence, in the case of levers, the term mechanical advantage is defined as the ratio of load and effort or the ratio of the output force and the input force.

TIPS: If you want a generic definition of the mechanical advantage of simple machines then you must not skip this tutorial on this site: what is mechanical advantage?

What is the Mechanical Advantage formula of a lever?

We have 2 equations or formulas for the MA of a lever.

1> Mechanical Advantage formula #1
Mechanical Advantage of lever = load / effort = load divided by effort
=> MA= L/E

2>Mechanical Advantage formula #2
Mechanical Advantage of lever = Effort Arm / Load Arm = effort arm divided by load arm
=> MA= EA /LA

Thus the mechanical advantage of a lever formula or equation is expressed either as the (i) ratio of load and effort or by the (ii) ratio of the effort arm and load arm.

Related study: MA of an inclined plane

We have 2 equations or formulas for the MA of a lever.

1> Mechanical Advantage formula #1
Mechanical Advantage of lever = load / effort = load divided by effort
=> MA= L/E

2>Mechanical Advantage formula #2
Mechanical Advantage of lever = Effort Arm / Load Arm = effort arm divided by load arm
=> MA= EA /LA

Thus the mechanical advantage of a lever formula or equation is expressed either as the (i) ratio of load and effort or by the (ii) ratio of the effort arm and load arm.

How to calculate the mechanical advantage of a lever? | How to find the ma of lever?

Either of the following 2 equations can help us to calculate the Mechanical Advantage(MA) of a lever.

i) MA of lever = load / effort.
First, we need to measure the load overcome by the lever and the effort applied to it. And then we need to calculate the ratio of these two parameters to calculate the mechanical advantage of the lever.

ii) MA of lever = Effort Arm / Load Arm = EA /LA.
In this case, we need to measure the effort arm length (fulcrum to effort distance) and the load arm length (fulcrum to load distance). Then we have to take their ratio to find the mechanical advantage of the lever.

Related study: MA of wedge

Either of the following 2 equations can help us to calculate the Mechanical Advantage(MA) of a lever.

i) MA of lever = load / effort.
First, we need to measure the load overcome by the lever and the effort applied to it. And then we need to calculate the ratio of these two parameters to calculate the mechanical advantage of the lever.

ii) MA of lever = Effort Arm / Load Arm = EA /LA.
In this case, we need to measure the effort arm length (fulcrum to effort distance) and the load arm length (fulcrum to load distance). Then we have to take their ratio to find the mechanical advantage of the lever.

What is a lever?

A lever is a simple machine that is basically a rigid rod that can rotate on a point (called pivot or fulcrum) on itself.
Examples of levers: seesaw, scissors, tweezers, stapler

To understand this a little more we should have at least a basic understanding of the lever structure. So let’s get that in the next paragraph.

How does the lever work?

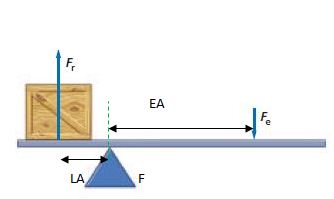
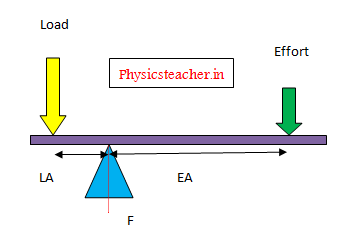
As said, a lever is a rigid rod that can rotate on a point or pivot. This pivot is called Fulcrum (F).
Now how it operates?

1> A force or effort(Fe) is applied at a point of the lever rod depending on the type of the lever. This effort is the input force.

2> The Lever transforms the input force either by amplifying it or by changing its direction and exerts an output force. This output force is called the Resistance force (Fr).

Note that, this output force is actually responsible to lift the Load. So you can say that magnitude wise the Resistance force is equal to the Load which the lever is capable to overcome for the given Effort. The load to be lifted is kept at a different point on the same rod or lever.

Here we can say that a lever is used to lift a load by applying a force or effort.

We will use the term LOAD to refer to the resistance force in the next paragraphs.

Refer to the diagram above to get an idea.
Here Fe is the applied force or Effort and Fr is the resistance force. This Fr lifts the Load.

Related study: MA of wheel and axle

What is the Effort Arm of a lever?

The length between the Effort and Fulcrum of a lever is called Effort Arm (EA)

Effort Arm formula

Effort Arm formula = Mechanical advantage x Load Arm length

What is the Load Arm of a lever?

The length between the Load and the Fulcrum of a lever is called Load Arm (LA).

Load Arm formula

Load Arm = Effort Arm length/ Mechanical advantage

How can we derive the Mechanical Advantage formula of a lever? | Derivation of the formula

A lever provides leverage to its users by amplifying the applied force or by providing comfort or convenience to do some specific activities.

The mechanical advantage of a lever is the amplification factor of a lever. It’s the ratio of Load and Effort. Here for simplicity, we have used the symbols L and E for load and effort respectively.

Mechanical Advantage formula of a lever = Load lifted/Effort applied= L/E ………………(equation 1)

In the diagram below, you can see that Effort(E) is trying to provide a CW (Clock Wise) rotation to the lever rod. On the contrary, Load L (the weight to be lifted, say) is trying to give an ACW (Anti Clock Wise) rotation to the rod.

In the balanced condition or equilibrium of a lever, the following condition is satisfied:
– If the lever is in rotational equilibrium then the Net torque is zero, which means, clockwise torque on the lever rod = anticlockwise torque on the lever rod.

 We know that torque is the cross product of force and lever arm.
Here as per the diagram, EA * E = LA * L

i.e., Effort Arm * Effort = Load Arm * Load

=> Load / Effort = Effort Arm / Load Arm

As we know, Mechanical Advantage = Load/Effort

That means another expression of MA is obtained here which is the ratio of the effort arm length and the load arm length.

How can you increase the mechanical advantage of a lever?

So it’s clear that to avail of a mechanical advantage value of more than 1, EA (Effort Arm) has to be more than LA (Load Arm).

This means getting the mechanical advantage of a lever of more than 1
– the load should be nearer to the fulcrum (to have a smaller Load Arm) and
– the Effort should be applied farther from the fulcrum (to make the Effort Arm larger).

**For some class I levers (like crowbar) and for all class II levers, we get MA of more than 1 by following the above-said condition.

related: MA of the inclined plane with a formula

related: Scissors vs Shears – How blade length and handle length change MA and functionality

How do the first class and the second class levers help in general to lift the load?

Now remember that, Mech Advantage = Load/effort.
So making Mech Advantage more than 1 means Load lifted is more than the Effort Applied.
That means the input effort is multiplied and a load more than the applied Effort can be lifted by a lever.

This is possible by some class I levers like crowbar (where effort arm>load arm) and by all class II levers (as all class II levers have effort arm longer than load arm), making their MA more than one.

These selective class 1 levers (like crowbar) and all class 2 levers act as force multipliers and thus help in lifting a heavier load.

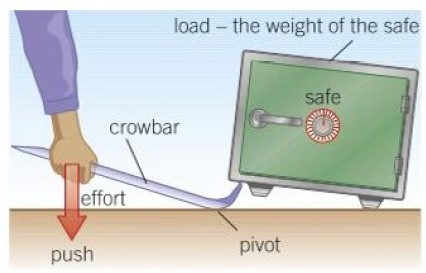
[ Find more examples of levers of all 3 types here ]

How does a class 3 lever have a Mechanical Advantage of less than one?

In the class III lever or third class lever, the effort is in between the fulcrum and load.

So the load arm basically takes up the entire length of the lever, starting from the load at one end to the fulcrum at the opposite end. While effort is in the middle of the fulcrum and load, the effort arm is just a part of the entire lever length.

Naturally, the load arm(LA) is always bigger than the effort arm(EA) for the class III lever.
As Mech Advantage is the ratio of EA and LA, so for class III (where LA>>EA) Mech advantage is always less than 1.

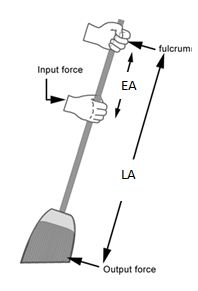
In spite of that, we use the class III lever in specific conditions where we apply more effort to lift a much lighter load but with greater ‘comfort’ and speed gain. Class III levers are all speed multipliers. They can’t help as force multipliers, but they can provide higher load velocity than effort velocity. (i.e. less displacement of effort can generate a bigger displacement of load)

class 2 lever mechanical advantage

In the class 2 lever, the load situates between the fulcrum and effort. As a result effort arm length is always more than the load arm length for the second class lever (class 2 lever). Hence, in the case of the class 2 lever, the mechanical advantage value is always more than 1.

Numerical – links

Solve numerical problems based on your understanding of the MA of a lever – go to this link on this site. MA of levers numerical

So in this post, we have discussed the mechanical advantage of a lever. Also, we have worked with the derivation of its formulae.

Hope you have liked it. So pls share this post with your friends as much as possible. See the related topic list below for relevant study material.

Reading the related topics helps:

MA of the inclined plane with formula


Velocity ratio


MA – Discussion with a bottle opener


MA <1, =1, >1 when these levers are used?