Kepler’s Laws of Planetary Motion

Johannes Kepler was an astronomer who established three laws that govern the motion of planets around the sun. These are known as Kepler’s laws of planetary motion. The same laws also describe the motion of satellites (like the moon) around the planets (like the Earth). In this post, we will state and briefly explain those laws.

Kepler’s laws of planetary motion are given below.

Kepler’s first law

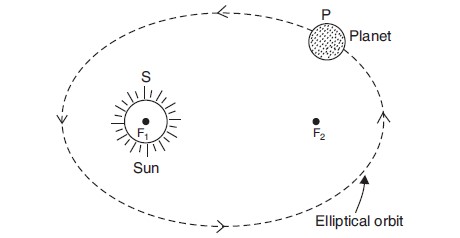
Kepler’s first law states that: The planets move in elliptical orbits around the sun, with the sun at one of the two foci of the elliptical orbit.

• This law means that the orbit (or path) of a planet around the sun is an ellipse (oval-shaped) and not an exact circle.
• An elliptical path has two foci, and the sun is at one of the two foci of the elliptical path (foci is the plural of focus).

This is shown in Figure 1. In Figure 1, planet P is moving around the sun S in an elliptical orbit. The elliptical orbit has two foci F1 and F2. The sun is located at the focus F1 (see Figure 1).

Kepler’s second law

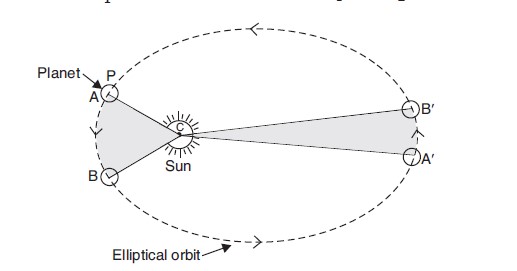
Kepler’s second law states that: Each planet revolves around the sun in such a way that the line joining the planet to the sun sweeps over equal areas in equal intervals of time.

• We know that a planet moves around the sun in an elliptical orbit with the sun at one of its foci.
• Now, since the line joining the planet and the sun sweeps over equal areas in equal intervals of time, it means that a planet moves faster when it is closer to the sun and moves slowly when it is farther from the sun.
• This point will become clear in Figure 2.

Kepler’s third law

Kepler’s third law states that: The cube of the mean distance of a planet from the sun is directly proportional to the square of the time it takes to move around the sun.
This law can be expressed as :
r³ ∞ T ²
or r³ = constant × T²
or r³/T² = constant
where r = mean distance of the planet from the sun
and T = time period of the planet (around the sun)