Lens Numericals class 10 | Thin lens numerical solved
Last updated on June 15th, 2023 at 04:18 pm
This post presents a set of Lens Numericals for class 10 with questions and answers. We will solve these Lens numerical problems with the help of lens sign convention and the lens formula.
Also, Read and revise: Sign convention of lens
Read here: Lens formula
Lens Numericals Class 10 – Solved
Question 1] An electric lamp and a screen are placed on the table, in a line at a distance of 1m. In what positions of a convex lens of the focal length of f = 21 cm will the image of the lamp be sharp?
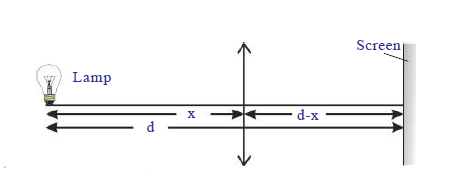
Solution:
The distance between the lamp and the screen is 100 cm and ‘x’ be the distance between the lamp and the lens. From fig, we have u = -x and v = 100-x, f = 21
1/v – 1/u = 1/f
=> 1/[100-x] – 1/[-x] = 1/21
=> 1/[100-x] + 1/[x] = 1/21Simplifying this equation, we get
x2-100x+2100=0
It is a quadratic equation. Hence we get two solutions. The solutions of the above equation are
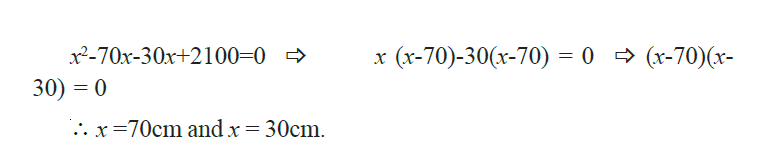
We can place the lens at a distance of 70cm or 30cm from the bulb, we get a sharp image.
Question 2] A convex lens of focal length 10 cm is placed at a distance of 12 cm from a wall. How far from the lens should an object be placed so as to form its real image on the wall ?
Solution.
Here, as per the problem statement, the real image is formed on the wall which is at a distance of 12 cm from the convex lens. This means that the distance of the image from the convex lens or image distance will be 12 cm. Since a real image is formed on the right side of the lens, this image distance will be positive.
Now, Image distance, v =+ 12 cm (A real image)
Object distance, u = ? (To be calculated)
Focal length, f = + 10 cm (It is a convex lens)
Putting these values in the lens formula :
1/v – 1/u = 1/f
=> 1/12 – 1/u = 1/10
=> Object distance u = -60 cm
Thus, the object should be placed at a distance of 60 cm in front of the convex lens. The minus sign
shows that the object is on the left side of the lens.
Question 3] If an object of 7 cm in height is placed at a distance of 12 cm from a convex lens of focal length 8 cm, find the position, nature, and height of the image.
Solution. First of all, we will find out the position of the image. This means we have to find out the image distance [the distance of the image from the lens].
Here, Object distance, u = – 12 cm (It is to the left of the lens)
Image distance, v =? (To be calculated)
Focal length, f = + 8 cm (It is a convex lens)
Putting these values in the lens formula :
1/v – 1/u = 1/f
=> 1/v – 1/[-12] = 1/8
=>Image distance, v = + 24 cm
Thus, the image is formed at a distance of 24 cm from the convex lens. The plus sign for image distance shows that the image is formed on the right side of the convex lens.
=>Only a real and inverted image is formed on the right side of a convex lens, so the image formed is real and inverted.
Let us calculate the magnification now. We know that for a lens: Magnification, m =v/u
Here, Image distance, v = 24 cm
Object distance, u = – 12 cm
So, m = 24/[-12] = -2
Since the value of the magnification is more than 1 (it is 2), so the image is larger than the object or magnified.
The minus sign for magnification shows that the image is formed below the principal axis. Hence the image is real and inverted.
Let us calculate the size of the image by using the formula: m=h2/h1
Here, Magnification, m = – 2 (Found above)
Height of object, h1 = + 7 cm (Measured upwards)
Height of image, h2 =? (To be calculated)
Now, putting these values in the above formula, we get :
-2 = h2/7
=> h2 = -2×7 = -14 cm
Thus, the height or size of the image is 14 cm. The minus sign shows that this height is in the downward direction, that is, the image is formed below the axis. Thus, the image is real and inverted.

