Spherical Lens class 10 | Spherical Lenses
Last updated on June 15th, 2023 at 04:34 pm
In this post, we have briefly discussed the topic of Spherical Lenses for class 10. Here we have covered what are spherical lenses, the types of spherical lenses, important terms related to spherical lenses, and image formation by spherical lenses. Here is our post on the ray diagrams of the images formed by spherical lenses.
Also, Read our Spherical Mirror class 10 notes.
What is Spherical Lens class 10 | Definition of Spherical Lens | What are spherical lenses
Spherical Lens – A transparent material bound by two surfaces, of which one or both surfaces are spherical, forms a spherical lens.
Spherical Lens – Types
Spherical lenses are of 2 types: Convex Lens and Concave Lens.
Convex Lens – When a lens has two spherical surfaces, bulging outwards, then it is called a double convex lens (or simply a convex lens. It is also known as a converging lens.
Concave Lens – A lens bounded by two spherical surfaces, curved inwards is known as a double concave lens (or simply a concave lens). It is also known as diverging lens because it diverges the light.
Spherical Lens – Important Terms for Class 10
Here, is a list of important terms related to Lens and its operation. The diagram below will help to understand the terms related to the characteristics of convex and concave lenses.
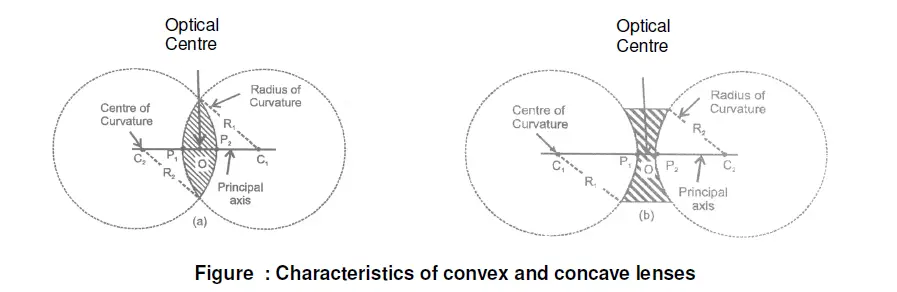
Centre of curvature of Lens class 10
A lens, either a convex lens or a concave lens has two spherical surfaces. Each of these surfaces forms a part of a sphere. The centres of these two spheres are called the centre of curvature represented by C1 and C2.
Principal axis of Lens
An imaginary straight line passing through the two centres of curvature is called the Principal axis of the lens.
Optical Centre of Lens
Optical Centre – If a ray of light is incident on a lens such that after refraction through the lens, the emergent ray is parallel to the incident ray, then the point at which the refracted ray intersects the principal axis is called the optical centre of the lens.
The central point of the lens is its optical centre (O). A ray of light, when passes through ‘O’ it remains undeviated i.e. it goes straight.
Aperture of Lens class 10
Aperture – It is the diameter of the circular boundary of the lens. The effective diameter of the circular outline of a spherical lens is called the aperture.
Focus of Lens class 10
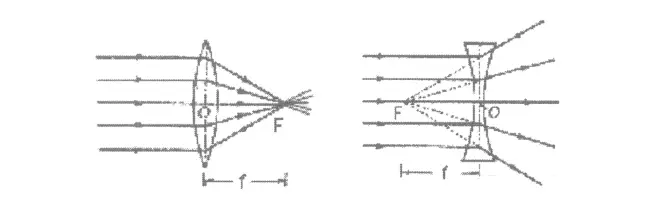
The focus of lens – In the case of a Convex lens, the Beam of light parallel to the principal axis, after refraction from the Convex lens, converges to the point on the principal axis, denoted by F, known as the Principal focus of a convex lens.
Similarly, In the case of a Concave lens, the Beam of light parallel to the principal axis, after refraction from the Concave lens, appears to diverge from a point on the principal axis, known as the principal focus F of a concave lens.
Focal Length
The distance between the principal focus and the optical centre is called the focal length.
The focus of a convex lens is real and that of a concave lens is virtual. Thus the focal length of a convex lens is taken as positive and the focal length of a concave lens is taken as negative.
Image Formation by Spherical Lens
Here, we will study the image formation feature of the Convex Spherical lens and Concave Spherical lens.
Image formed by a convex spherical lens – for different object positions
The details of the Image formed by a convex spherical lens, for different object positions are given in the table below:
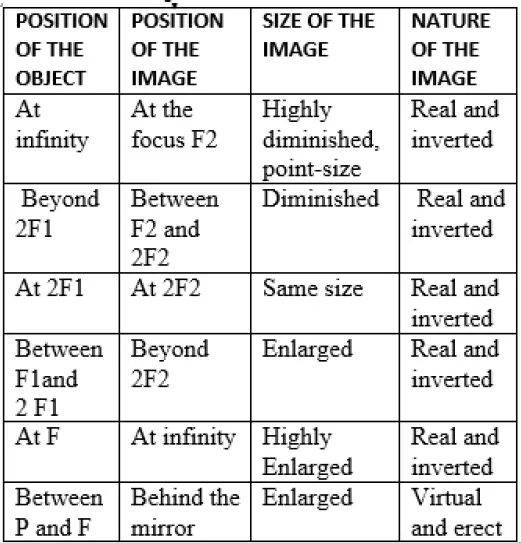
Also, read this post on the ray diagrams of the images formed by a convex lens.
Image formed by a concave spherical lens – for different object positions
The details of the Image formed by a concave spherical lens, for different object positions are given below:
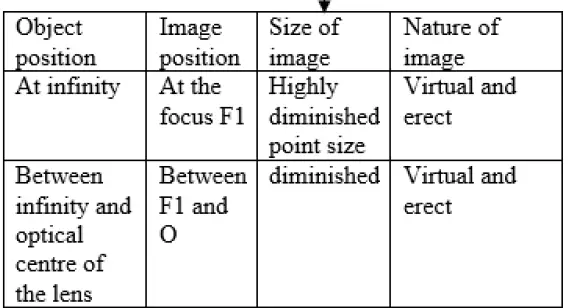
Also, read this post on the ray diagrams of the images formed by a concave lens.
Power of Lens
The degree of convergence or divergence of light rays achieved by the lens is known as the Power of the Lens (P). It is defined as the reciprocal of its focal length and it is expressed as P = 1/f.
SI unit of lens power is Dioptrer (D)
