Equipotential lines & surfaces in an electric field
In this post, we will define Equipotential lines and equipotential surfaces in an electric field. Then we will see their significance. Potential gradients for Equipotential lines and equipotential surfaces are shown in diagrams for uniform and radial electric fields.
Equipotential lines
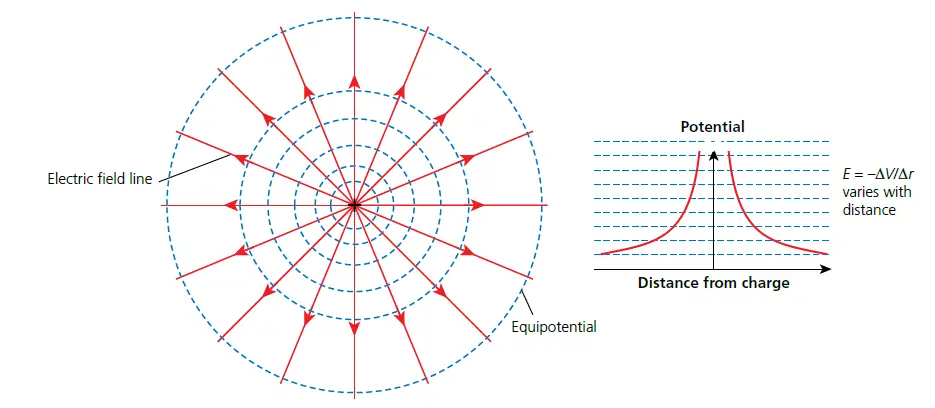
A line of equipotential is a line joining points of equal potential just like a contour line on a map joining points of equal height. Since E = −ΔV/Δr, the closer the lines of equipotential are the greater the potential gradient and so the greater the field strength.
Equipotential surface
An equipotential surface is a surface that joins points of equal potential, and therefore a surface on which the potential does not vary. This means that if you connected a wire between two points on the surface no current would flow between them.
features of equipotential surfaces
Note: Electric field lines are always at right angles to lines of equal potential and to equipotential surfaces.
No work is done in moving an electric charge along an equipotential surface.
equipotential lines for uniform and radial fields (diagrams)
Figure 1 & figure 2 below show equipotential lines for uniform and radial fields, respectively.
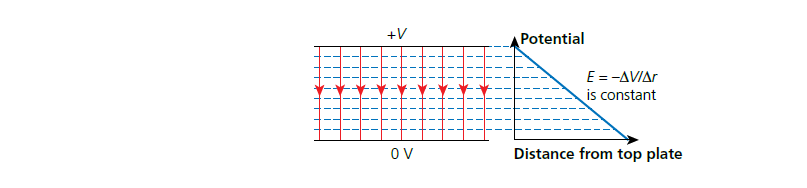
figure 1: Equipotential lines for uniform fields