coefficient of static friction (μs) = tan θ
In this post, we will see how the coefficient of static friction (μs) = tan θ, where θ is the angle of inclination where static friction becomes the highest. In other words, θ is the angle of inclination when friction equals the value of limiting friction. (The maximum possible frictional force before the object starts moving is called the Limiting Friction.)
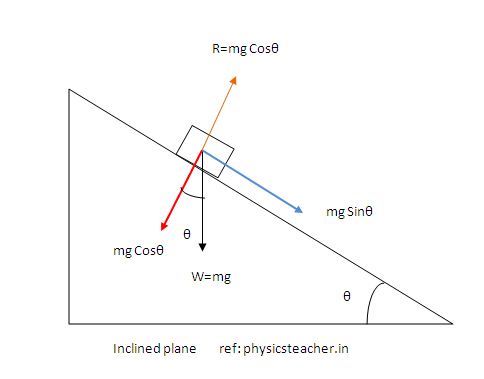
The “free-body” diagram of a block on an inclined plane (ramp) is shown in Figure 1.
The angle θ is assumed to be at its maximum value, that is, the friction force has its maximum value Fsmax=μs R = μs mg Cos θ.
As the block tends to slide downwards due to its weight component mg Sin θ, the friction will direct upwards along the slope.
When the friction equals limiting friction, i.e., the angle θ is assumed to be at its maximum value before the block starts sliding downwards, the net force along the inclined plane is Fnet= 0
=> mg Sin θ – Fsmax =0
=>mg Sin θ – μs mg Cos θ =0
=>mg Sin θ =μs mg Cos θ
=>μs = (mg Sin θ)/(mg Cos θ)
=>μs = tan θ (proved)
Read More:
