The Carnot Engine

Last updated on May 14th, 2022 at 02:06 pm

In this post, we will discuss the concepts of the Carnot engine. We will also cover subtopics like Assumptions made for the Carnot engine, the existence of the Carnot engine(if possible?), Laws of Thermodynamics & the Carnot Engine, Efficiency & temperature, etc.

During the early 19th century maximizing the efficiency of the heat engine was an important topic. The Frenchman Sadi Carnot (1796-1832), analyzed the characteristics of an ideal heat engine.

The Carnot engine is a mathematical abstraction conceived by assuming physical processes that are impossible. Carnot was able to establish the upper limit of a heat engine’s efficiency by using his idealized model.

---

Assumptions made for the Carnot engine

• Carnot engine is an ideal heat engine that assumes that each process the engine performs is reversible.
• Carnot assumed his reversible engine could perform with maximum efficiency if an ideal engine made use of isothermal and adiabatic processes only.
• All processes were assumed to occur infinitely slowly, having the engine move from one approximate equilibrium state to the next, thus ensuring that the processes could be reversed.

Carnot engine can’t exist in reality

Carnot engine of course could never exist. The idea of constructing infinitely slow processes is impossible. The Carnot engine, as we will see, is just a useful conceptual idea for establishing the upper limit of a heat engine’s efficiency for a given pair of high and low temperatures.

Efficiency & Temperature

Carnot was able to show that at maximum efficiency the high Q_H and low Q_L energy transfers were proportional to the high T_H and low T_L temperatures under which the engine operated.

We can therefore write efficiency e=(1 − (T_L / T_H))×100% where T is in kelvins.

This was a very important result because it showed, all things being equal, that those substances that could produce the highest temperature when burning would produce greater efficiency.

Laws of Thermodynamics & Carnot Engine

A simplified version of the Second Law of Thermodynamics according to Carnot is that it is impossible to convert heat completely into work in a cyclic heat engine; there is always some heat output.

Note that the First Law of Thermodynamics would allow a heat engine to have no heat output, the heat input would equal the work done.

The Second Law can be shown in the diagram below where the input heat is taken from a “reservoir” that maintains a constant high temperature and the output heat goes to a second reservoir at a constant low temperature.

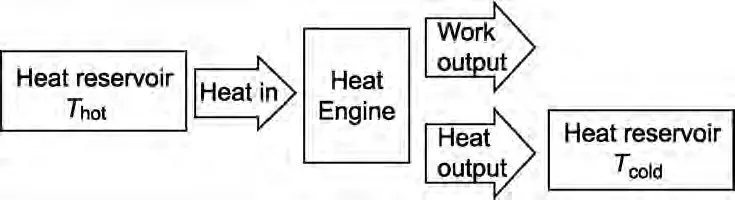
For example, a steam turbine gets its heat from high-temperature steam and puts its output heat into a much colder lake or river.