Carnot cycle processes of Carnot engine
Last updated on May 16th, 2022 at 09:01 pm
The Carnot cycle represents the cycle of processes for a theoretical heat engine with the maximum possible efficiency. Such an idealized engine is called a Carnot engine. Here in this post, we present a brief idea of the Carnot cycle processes, Carnot engine efficiency, and also we solve here a numerical problem related to the Carnot engine.
Carnot Cycle processes
The Carnot cycle represents the cycle of processes for a theoretical heat engine called a Carnot engine. This engine ideally is with the maximum possible efficiency.
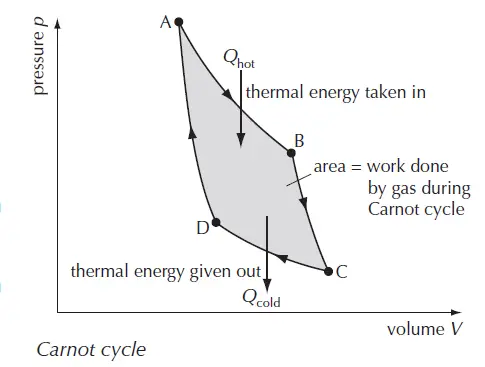
Carnot cycle consists of an ideal gas undergoing the following processes: (refer to figure 1 for A, B, C, and D nodes of the Carnot cycle)
- Isothermal expansion (A →B)
- Adiabatic expansion (B →C)
- Isothermal compression (C →D)
- Adiabatic compression (D →A)
The area of ABCD provides the work done by the gas during the Carnot cycle.
Efficiency of Carnot engine
The temperatures of the hot and cold reservoirs fix the maximum possible efficiency that can be achieved.
The efficiency of a Carnot engine can be shown to be: ec= 1 – TC/TH, (Here, T in Kelvin)
% efficiency of a Carnot engine: %ec= [1 – TC/TH] x 100%
Numerical problem related to Carnot engine and Carnot cycle
Q ) An engine operates at 300 °C and ejects heat to the surroundings at 20 °C. Find out the maximum possible theoretical efficiency.
Solution:
TC = 20 + 273 k = 293 K
TH = 300 + 273 k = 573 k
The maximum possible theoretical efficiency = ec= 1 – TC/TH = 1 – 293/573 = 0.49
Hence, %efficiency = 49%

