Electric potential energy – study notes
Last updated on January 26th, 2022 at 01:32 pm
In this post, we will see how a charge gains or loses Electric potential energy when it moves around in an electric field. We will also derive the equation of the change in the electric potential energy of a charge in an electric field. Also, we will derive the formula of the velocity of a charge in an electric field, as its electric potential energy gets converted to kinetic energy.
Electrical potential energy – concepts
- The electric potential energy of a charge at any point, EP, is the amount of energy needed to bring the charge from infinity to that point.
- When charges are moved in electric fields energy is transferred (work is done), unless the movement is perpendicular to the direction of the force (and field). We describe these as changes in electric potential energy.
- To move opposite charges apart, work has to be done against the electric forces attracting them together. That is, energy must be transferred to the system.
- Conversely, when electric forces pull like charges closer together, energy will be transferred from electric potential energy.
- More generally, we consider that electric potential energy is stored in any system of charges because, at some time in the past, work was done when the charges moved to their present positions.
- If we wanted to calculate the total electric potential energy of an electrostatic system, we would need to be clear about an agreed zero for electric potential energy: a system of static charges has zero electric potential energy if they are so far apart (an infinite distance) that there are zero electric forces between them.
- The electric potential energy stored between opposite charges is negative (like gravitational potential energy) because energy would need to be supplied to completely separate them and produce a system with zero energy. The electric potential energy stored between like charges is positive.
Electric potential energy & Energy difference in an electric field
When a charge is placed in an electric field, it feels a force. This means that if it moves around in an electric field then work will be done. As a result, the charge will either gain or lose electric potential energy.
Electric potential energy is the energy that a charge has as a result of its position in an electric field.
This is the same idea as a mass in a gravitational field. If we lift a mass up, its gravitational potential energy increases. If the mass falls then its gravitational potential energy decreases.
In the example below a positive charge is moved from position A to position B. In this case, as per figure 1, Position B has higher electric potential energy compared to position A. This results in an increase in electric potential energy. In other words, the sample positive charge will gain electric potential energy.
Calculate the change in Electric potential energy | formula of Electric potential energy change
Since the field is uniform in this case, the force is constant. This makes it is very easy to calculate the work done.
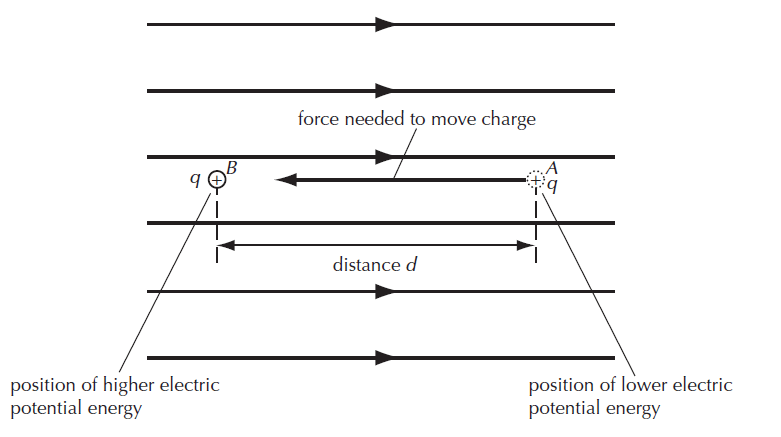
Change in electric potential energy in the sample charge
= force on the charge × distance traveled by the charge
= E q × d
The formula of change in Electric potential energy = E q × d
Velocity of the charge in an electric field
In the example above the electric potential energy at B is greater than the electric potential energy at A. We would have to put in this amount of work to push the sample positive charge from A to B.
If we let go of the sample positive charge at B it would be pushed (repelled) by the electric field. This push would accelerate it so that the loss in electrical potential energy would be the same as the gain in kinetic energy.
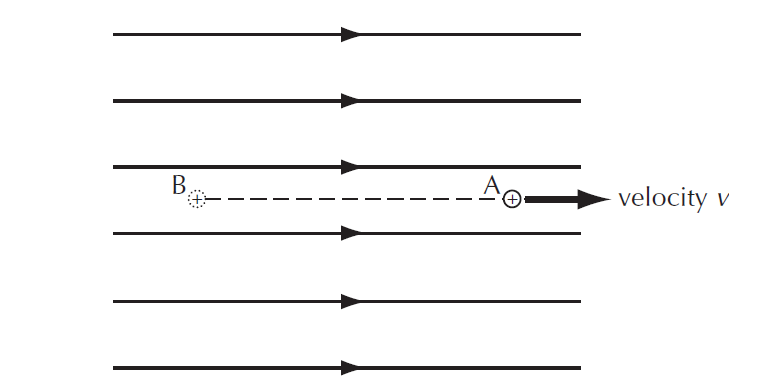
The gain in kinetic energy = loss in electric potential energy
(1/2) m v2 = E q d
m v2 = 2 E q d
∴ Velocity of the charge = v = √( 2 E q d /m)

